Machine Learning for Fluid Dynamics: Patterns

 

The data set he mentions is Johns Hopkins Turbulence Databases. Many hundreds of Terabytes of direct numerical simulations with different governing equations and boundary conditions.

Hybrid Parallelism Approaches for CFD

This previous post, Plenty of Room at Exascale, focuses on one specific commercial approach to scaling CFD to large problems on heterogeneous hardware (CPU & GPU) clusters. Here's some more references I found interesting reading on this sort of approach.

Strategies

Recent progress and challenges in exploiting graphics processors in computational fluid dynamics provides some general strategies for using multiple levels of parallelism accross GPUs, CPU cores and cluster nodes based on that review of the literature:

• Global memory should be arranged to coalesce read/write requests, which can improve performance by an order of magnitude (theoretically, up to 32 times: the number of threads in a warp)
• Shared memory should be used for global reduction operations (e.g., summing up residual values, finding maximum values) such that only one value per block needs to be returned
  
• Use asynchronous memory transfer, as shown by Phillips et al. and DeLeon et al. when parallelizing solvers across multiple GPUs, to limit the idle time of either the CPU or GPU.
• Minimize slow CPU-GPU communication during a simulation by performing all possible calculations on the GPU.

Plenty of Room at Exascale

The folks at Envenio have posted an interesting marketing video on their solver.

A One-Equation Local Correlation-Based Transition Model

This article is available for free download until 15 Oct 2015, h/t ANSYS blog.

Here's the Abstract:

A model for the prediction of laminar-turbulent transition processes was formulated. It is based on the LCTM (‘Local Correlation-based Transition Modelling’) concept, where experimental correlations are being integrated into standard convection-diffusion transport equations using local variables. The starting point for the model was the γ-Re θ model already widely used in aerodynamics and turbomachinery CFD applications. Some of the deficiencies of the γ-Re θ model, like the lack of Galilean invariance were removed. Furthermore, the Re θ equation was avoided and the correlations for transition onset prediction have been significantly simplified. The model has been calibrated against a wide range of Falkner-Skan flows and has been applied to a variety of test cases.

Keywords: Laminar-turbulent transition, Correlation, Local variables
Authors: Florian R. Menter, Pavel E. Smirnov , Tao Liu, Ravikanth Avancha

Transition location, and subsequent turbulence modeling remain the largest source of uncertainty for most engineering flows. Even for chemically reacting flows the source of uncertainty is often less the parameters and reactions for the chemistry, and more the uncertainty in the fluid state driven by shortcomings in turbulence and transition modeling.

UberCloud HPC Experiment

I think I originally saw a link for the UberCloud HPC Experiment on one of the "This week in CFD" posts on Another Fine Mesh. It is a market research exercise to see how people would use cloud computing (platform as a service, software as a service) for their high performance computing workloads. The focus of the experiment is on the difference between enterprise work-loads and high-performance or scientific computing work-loads. Here's some of the introduction describing the research:

We found that, in particular, small- and medium-sized enterprises in digital manufacturing would strongly benefit from HPC in the Cloud (or HPC as a Service). The major benefits they would realize by having access to additional remote compute resources are: the agility gained by speeding up product design cycles through shorter simulation run times; the superior quality achieved by simulating more sophisticated geometries or physics; and the discovery of the best product design by running many more iterations. These are benefits that increase a company’s competitiveness.

Tangible benefits like these make HPC, and more specifically HPC as a Service, quite attractive. But how far away are we from an ideal HPC cloud model? At this point, we don’t know. However, in the course of this experiment as we followed each team closely and monitored its challenges and progress, we gained an excellent insight into these roadblocks and how our teams have tackled them.
UberCloud HPC Experiment: Compendium of Cases

Each of their teams has an industry user, a resource provider, a software provider, and an HPC expert.

This part on applications is interesting:

By far, computational fluid dynamics (CFD) was the main application run in the cloud by the Round 1 and Round 2 teams – 11 of the 25 teams presented here concentrated their efforts in this area.

I think this really helps make the case for open source CFD codes:

In addition to unpredictable costs associated with pay-per-use billing, incompatible software licensing models are a major headache. Fortunately many of the software vendors, especially those participating in the Experiment, are working on creating more flexible, compatible licensing models, including on-demand licensing in the cloud.

Paying a per-core license makes no sense for these large jobs.

One of the interesting use cases was from Team 30 who used an open source stack (Elmer, CAELinux) on top of Amazon Web Services Elastic Compute Cloud.

A Defense of Computational Physics

This is a defense a long time in the making (h/t Dan Hughes). Patrick Roache has done short articles along a similar vein defending the Computational Physics enterprise against what amounts to an empty nihilism that seems to be popular among academics.

Here is the publisher's description,
Karl Popper is often considered the most influential philosopher of science of the first half (at least) of the 20th century. His assertion that true science theories are characterized by falsifiability has been used to discriminate between science and pseudo-science, and his assertion that science theories cannot be verified but only falsified have been used to categorically and pre-emptively reject claims of realistic Validation of computational physics models. Both of these assertions are challenged, as well as the applicability of the second assertion to modern computational physics models such as climate models, even if it were considered to be correct for scientific theories. Patrick J. Roache has been active in the broad area of computational physics for over four decades. He wrote the first textbooks in Computational Fluid Dynamics and in Verification and Validation in Computational Science and Engineering, and has been a pioneer in the V&V area since 1985. He is well qualified to confront the mis-application of Popper's philosophy to computational physics from the vantage of one actively engaged and thoroughly familiar with both the genuine problems and normative practice.
Here is a short excerpt from one of Roache's papers that gives a flavor of the argument he is addressing,

In a widely quoted paper that has been recently described as brilliant in an otherwise excellent Scientific American article (Horgan 1995), Oreskes et al (1994) think that we can find the real meaning of a technical term by inquiring about its common meaning. They make much of supposed intrinsic meaning in the words verify and validate and, as in a Greek morality play, agonize over truth. They come to the remarkable conclusion that it is impossible to verify or validate a numerical model of a natural system. Now most of their concern is with groundwater flow codes, and indeed, in geophysics problems, validation is very difficult. But they extend this to all physical sciences. They clearly have no intuitive concept of error tolerance, or of range of applicability, or of common sense. My impression is that they, like most lay readers, actually think Newton’s law of gravity was proven wrong by Einstein, rather than that Einstein defined the limits of applicability of Newton. But Oreskes et al (1994) go much further, quoting with approval (in their footnote 36) various modern philosophers who question not only whether we can prove any hypothesis true, but also “whether we can in fact prove a hypothesis false.” They are talking about physical laws—not just codes but any physical law. Specifically, we can neither validate nor invalidate Newton’s Law of Gravity. (What shall we do? No hazardous waste disposals, no bridges, no airplanes, no...) See also Konikow & Bredehoeft (1992) and a rebuttal discussion by Leijnse & Hassanizadeh (1994). Clearly, we are not interested in such worthless semantics and effete philosophizing, but in practical definitions, applied in the context of engineering and science accuracy.
Quantification of Uncertainty in Computational Fluid Dynamics, Annu. Rev. Fluid. Mech. 1997. 29:123–60

Interesting Developments in the Numerical Python World

From Travis Oliphant by way of the Planet Scipy feed:

Hello all,

There is a lot happening in my life right now and I am spread quite thin among the various projects that I take an interest in. In particular, I am thrilled to publicly announce on this list that Continuum Analytics has received DARPA funding (to the tune of at least $3 million) for Blaze, Numba, and Bokeh which we are writing to take NumPy, SciPy, and visualization into the domain of very large data sets. This is part of the XDATA program, and I will be taking an active role in it. You can read more about Blaze here: http://blaze.pydata.org. You can read more about XDATA here: http://www.darpa.mil/Our_Work/I2O/Programs/XDATA.aspx

I personally think Blaze is the future of array-oriented computing in Python...

Passing the torch of NumPy and moving on to Blaze

OpenFOAM and FEniCS Fedora Install Notes

Notes on installing OpenFOAM and FEniCS from source on Fedora 14.

Both projects implement ideas similar to A Livermore Physics Applications Language (NALPAL, why ALPAL): take high-level descriptions of partial differential equations and automatically generate code to solve them with numerical approximations based on finite-volume (OpenFOAM) or finite-element (FEniCS) methods.

Useful Links

• FEniCS install from source

• OpenFoam source pack

• open foam uses paraview, paraview.org
• open foam uses wmake, which is a script that comes with the installation

• FEniCS uses cmake

Steps for OpenFOAM

1. Install Fedora packages for paraview, cmake, flex, qt, zlib.
   [root@deeds foo]$ yum -y install paraview cmake flex qt-devel libXt-devel zlib-devel zlib-static scotch scotch-devel openmpi openmpi-devel
   You probably already have gnuplot and readline installed, if not, install those too.
2. Unpack the OpenFOAM tarball:
   [jstults@deeds OpenFOAM]$ tar -zxvf OpenFOAM-2.0.1.gtgz
3. Add the environment variable definitions to the bashrc file
   source $HOME/OpenFOAM/OpenFOAM-2.0.1/etc/bashrc
[jstults@deeds OpenFOAM]$ source ~/.bashrc
4. Run the OpenFOAM-X.y.z/bin/foamSystemCheck script, you should get something that says, "System check: PASS", "Continue OpenFOAM installation."
5. Go to the top-level directory, since you defined the proper environment variables that is something like
   [jstults@deeds OpenFOAM]$ cd $WM_PROJECT_DIR
6. Make it
   [jstults@deeds OpenFOAM-X.y.z]$ ./Allwmake
7. Various Consequences ensue...

Steps for FEniCS

Required components: Python packages FFC, FIAT, Instant, Viper and UFL, and Python/C++ packages Dolfin and UFC

1. Install things packaged for Fedora
   [root@deeds FEniCS]$ yum -y install python-ferari python-instant python-fiat
2. Download the other components from launchpad, and install using
   [jstults@deeds FEniCS]$ python setup.py install --prefix=~/FEniCS
   for the Python packages, and
   [jstults@deeds FEniCS]$ cmake -DCMAKE_INSTALL_PREFIX=$HOME/FEniCS ./src
[jstults@deeds FEniCS]$ make
[jstults@deeds FEniCS]$ make install
   for the C++/Python packages (DOLFIN and UFC).

OR, do it automatically if you have root and internet access (I still haven't got this to work: a bit of buffoonery on my part, problems finding boost libraries).

1. Download Dorsal
   
2. Run the script
   [jstults@deeds FEniCS]$ ./dorsal.sh
3. Execute the yum command in the output from the script in another terminal.
   [root@deeds FEniCS]$ yum install -y redhat-lsb bzr bzrtools subversion \ libxml2-devel gcc gcc-c++ openmpi-devel openmpi numpy swig wget \ boost-devel vtk-python atlas-devel suitesparse-devel blas-devel \ lapack-devel cln-devel ginac-devel python-devel cmake \ ScientificPython mpfr-devel armadillo-devel gmp-devel CGAL-devel \ cppunit-devel flex bison valgrind-devel
   I also installed the boost-openmpi-devel and boost-mpich2-devel packages as well. MPI on Fedora is kind of a mess. I added these two lines to my bashrc:
   module unload mpich2-i386
module load openmpi-i386
   
4. When the packages are installed, go back to the terminal running dorsal.sh and hit ENTER.

I ended up downloading the development version of dorsal to get the latest third-party software built, because it's so easy:
[jstults@deeds dorsal]$ bzr branch lp:dorsal
Pretty darn slick, Yea for distributed version control systems! Boo for dependency hell!

FEniCS is currently under heavy development towards a 1.0 release, so I expect to be able to build it on Fedora 14 Real Soon Now ; - )

Update: Johannes and friends got me straightened out.

Notre Dame V&V Workshop

The folks at Notre Dame are putting on a Verification and Validation Workshop. The preliminary agenda is up on the workshop site.

The purpose of the workshop is to bring together a diverse group of computational scientists working in fields in which reliability of predictive computational models is important. Via formal presentations, structured discussions, and informal conversations, we seek to heighten awareness of the importance of reliable computations, which are becoming ever more critical in our world.

The intended audience is computational scientists and decision makers in fields as diverse as earth/atmospheric sciences, computational biology, engineering science, applied mechanics, applied mathematics, astrophysics, and computational chemistry.

It looks very interesting. Unfortunately, I don't think I'll be able to attend. Hopefully they will post posters and papers. Update: I was able to attend. They will be posting the presenters' slides. I will put up some of my notes when they get the slides up.

Computational Explosive Astrophysics

I got an update with an interesting set of slides on adaptive mesh refinement recently. I've always been more of a moving mesh kind of guy, but lots of people find the AMR approach useful. The slides are for a summer course on Computational Explosive Astrophysics. They have an index for the lecture notes where those slides came from. Last year's course was Galaxy Simulations.

Why ALPAL

Really it's "why use symbolic math programs to develop number crunching software," but these are from the doc_282 in the ALPAL docs (my emphasis).

• First, physics code could be generated and modified to incorporate new physics and features at a much greater speed than occurs with present codes. Such a language would directly foster improvements in the physics models employed, as well as teh numerical methods used to approximate these models. Two reasons point out the need to experiment with numerical methods for a given set of integro-differential equations. First, as a direct consequence of the paucity of mathematical theorems that constructively characterize partial differential equations (PDEs) in general, there is no means of determining what approximation technique will most faithfully capture the solution. Second, in almost all cases, analysis of an approximation technique is limited to idealized linear problems, so the stability and convergence properties of applying a given approximation technique to actual set of PDEs is unknown. Thus, the optimal algorithm for solving any given PDE or set of PDEs is not known, and any tool to aid the computational physicist must be capable of dealing with many different numerical algorithms and methods.
• Second, much of the drudgery and concomitant errors in constructing simulation codes would be eliminated by such a language. Large amounts of uninteresting algebra are associated with both the development of appropriate physical models and the discrete versions of the these models on a computer. If the algebraic work involved could be largely automated, computational physicists could spend a great deal more time doing the physics they were trained to do.
• Third, a more natural way of describing the physics model is possible with such a language. Errors in the modeling and numerical approximation process would become more obvious, thereby reducing the number of errors in the simulation code.
• Fourth, it becomes possible to automate the computation of Jacobian matrices both for linear and nonlinear problems. Not only would this automatic calculation greatly reduce the number of algebraic errors commited for those cases that solve linear systems of equations (with or without a nonlinear solver0, but it would make possible a large number of implicit techniques for situations where it has just not been feasible to use them in the past.
• Fifth, such a language could fulfill the need to optimize the very expensive computation that goes on in simulation codes. While a competent scientis can do a good job of optimizing a simple simulation code, the complexity of this task for large simulation codes is beyond the capabilities of even the most skilled scientist. Moreover, optimizing a code is a mundane task that once again does not reward the scientist in his primary pursuit. Optimization becomes an even more critical issue on non-scalar computer architectures such as the CRAY-XMP or an ultracomputer. A high-level view of how to vectorize and/or parallelize a given algorithm (or meta-algorithm) on one of these supercomputers is crucial so the scientist can substantially improve the cost-effectiveness of a simulation on that computer. In principle, a language like ALPAL can provide such a view.
• Sixth, since the cost of developing simulation codes is great, especially for new machine architectures, this language could be used to dramatically cut development costs. This is true whether a simulation code is being created for a new machine or whether it is being ported from a previously used computer. Experience with vector computers over the past decade at LLNL has taught this lesson well. More recently, some simulation codes have been ported to the CRAY-XMP, with use being made of its distributed computing capability. This porting to a distributed computer has required an even larger investment of manpower. These large manpower development costs will be repeated many times because a great variety of parallel computers are now appearing, and because parallel computing is a far greater technical challenge than even vector computing.
• Seventh, more complete and coherent documentation can be developed with such a language. In fact, a journal-style specification of a code can provide many details that are not generally provided in a journal article about the code. The journal-style specification is expressly designed for readability, wheras the text of a traditional simulation code is not. This is so because it is impossible to express high-level mathematical concepts such as derivatives and integrals together with their numerical approximations in Fortran or any other conventional high-level language.

NALPAL: Not A Livermore Physics Applications Language

Background and Motivation

The problem I am interested in: leverage high-level symbol manipulation capabilities in a computer algebra system (CAS) to generate compile-able code for number crunching. More specifically, I am interested in generating routines for numerical partial differential equation (PDE) solvers. This is not a new idea, significant work was accomplished starting in the early 1980s [1, 2, 3], continued into the late ’80s [4, 5, 6], and early ’90s [7]. However, those capabilities have not been consolidated and formally incorporated into my open-source CAS of choice, Maxima (though there is fairly recent work implementing similar ideas for Mathematica [8, 9]). The early work [1] quotes Hamming’s Turing Award speech [10] for motivation:

We seem not to be able to use the machine, which we all believe is a very powerful tool for manipulating and transforming information, to do our own tasks in this very field. We have compilers, assemblers, monitors, etc. for others, and yet when I examine what the typical software person does, I am often appalled at how little he uses the machine in his own work.

I had been thinking about this problem for a while because of my interest in method of manufactured solutions (MMS) for code verification. I thought things were really going to take off when I came across Cook’s 1990 technical report describing code generation for PDE solvers using A Livermore Physics Applications Language (ALPAL), which was built on top of DOE-MACSYSMA. ALPAL aimed to be a general purpose domain specific language for turning symbolic descriptions of PDEs into code. Here’s a solution to the problem already developed! Of course, it couldn’t be that easy. I asked the Maxima mailing list if anyone knew what became of this effort: ALPAL question to Maxima list, and ended up answering my own question by getting a hold of some of the old ALPAL devs: ALPAL answer to the list. Unfortunately, there is a long history behind the divergence between different versions of MACSYMA (and different groups of developers) that mitigates against this old code ever working with the fork that became Maxima (should an archive of the source ever actually turn up, update: it did, see comment) [11, 12, 13].

As you may have guessed from this post’s title, and the difficulties described in the previous paragraph, I’ve decided to pursue a more toolbox approach rather than (re)implementing a domain specific language and associated decision logic. The working title for my toolbox of utilities will be NALPAL, both as a nod to the valuable historical work in this area, and an indication of the path not taken.

Wirth categorizes three main approaches to systems for numerical PDE solution: black-box systems, subroutine packages, and code generation aids [1]. Black-box systems are intended for the novice user, and tend to be constrained to very specific problem types or incorporate a great deal of decision logic. Subroutine packages provide reusable building blocks, but require more knowledge and coding on the part of the user, and tend to remain problem specific. Code generation aids require the user to be an expert in numerical analysis, and tend not to automate any of the analytical work that precedes the code generation step.

Wirth’s suggested approach is a Unix-like toolbox approach where standard subroutine libraries are used when it makes sense to do so, and utilities for doing custom code generation are written in the CAS environment. The alternative is to create a full language, and incorporate the semantics and decision logic to automate the entire process for the novice user. The work of Wirth, Steinberg and Roache is a good example of the former approach, and Cook’s work on ALPAL is an example of the latter (though his early work [3] is more along the lines of the toolbox approach, going so far as to say “the viewpoint taken is that one should be able to start with integro-differential equations and end up with optimal FORTRAN code segments. The key in achieving this goal was to tackle only the specific algebraic problem-i at hand, and not to attempt to provide tools to cover every conceivable numerical scheme.”). The toolbox approach keeps more of the work for the problem solver in set-up/tear-down/customization, while the language approach loads more of the burden on to the domain specific language developer. Wirth’s second objective sums up well the approach that I think makes the most sense (emphasis original):

Build productivity enhancing tools of broad applicability for the expert user so that efficient, special purpose PDE codes can be built reliably and quickly, rather than attempt to second guess the expert and build general purpose PDE codes (black box systems) of doubtful efficiency and reliability.

There are still useful things to learn from ALPAL even if we have chosen the less ambitious road, since the problem being solved is the same. A basic description of the ALPAL use-case [7]:

1. Take as input a PDE description, along with boundary and initial condition definitions
2. Discretize the PDE
3. Analyze the result (e.g. for stability)
4. Calculate the Jacobian (needed for Newton methods in implicit time-integration or non-linear boundary value problem (BVP)s)
5. Generate code

Even if we don’t have a full-featured language, the user of our set of utilities will still be interested in accomplishing largely these same steps. In fact, Wirth’s early work gives these steps (reproduced here verbatim) [1]:

1. Manipulate the set of partial differential equations to cast them into a form that is amenable to numerical solution. For vector PDEs, this might include vector differential calculus operations and reexpression in scalar (component) form, and the application of a linearization approximation for non-linear PDEs.
2. Discretize the time and space domain, and transform the partial differential operators in the PDEs into finite difference operators. This transforms the partial differential equations into a set of algebraic equations. A multitude of possible transformations for the differential operators are possible and the boundary conditions for the PDEs also must be appropriately handled. The resulting difference equations must be analyzed to see if they form an accurate and numerically stable approximation of the original equation set. For real world problems, this analysis is usually difficult and often intractable.
3. After choosing a solution algorithm from numerical linear algebra, the finite difference equations and boundary conditions are coded in a programing language such as FORTRAN.
4. The numerical algorithm is then integrated with code for file manipulations, operating system interactions, graphics output, etc. forming a complete computer program.
5. The production program is then executed, and its output is analyzed, either in the form of numerical listings or computer-generated graphics.

Wirth goes on to say (emphasis added),

With continuing advances in computer technology, the last step in this process has become easier. For a given class of problems, answers can be calculated more quickly and economically. More importantly, harder problems which require more computational resources can be solved. But the first four steps have not yet benefited from advances in computer performance; in fact, they are aggravated by it.

Also, this additional bit of motivation from Chapter 5,

Taken together with the software described in other chapters, these tools allow the user to quickly generate a FORTRAN code, run numerical experiments, and discard the code without remorse if the numerical results are unsatisfactory.

This is similar in sentiment to the idea of numerical throw away code.

PDE Code Gen Recipes

With the problem background and motivation set, the rest of this post will focus on pulling out useful Maxima recipes demonstrated by folks who have generated FORTRAN from MACSYMA with intent to inflict grievous arithmurgical damage on hapless PDEs.

Much work is done in most of these articles from the 1980s to avoid array references and break up expressions by hand to reduce the computational cost in MACSYMA. Also, MACSYMA’s knowledge of the chain rule is not used for calculating the transformations because of an explosion in the number of terms [5], rather an identity for the derivative of a matrix inverse is used. A lot of this effort seems unnecessary today because speed and memory have improved so much. However, the basic approach and variables used to define the problem is still relevant (compare with this example of Burgers’ equation on a curvilinear grid):

  dep : [f, sigma]; /* the dependent variables */
  curvi : [xi, eta, zeta]; /* the curvilinear coordinates */
  indep : [x, y, z]; /* the independent variables */
  depends(curvi, indep);
  depends(dep, curvi);
  nn : length(indep);
  eqn : sum(diff(sigma * diff(f, indep[i]), indep[i]), i, 1, nn);

The result is rather large, but it illustrates Maxima’s knowledge of the chain rule. Of course, generally it is easiest to compute rather than for an arbitrary grid, so you need to make substitutions based on the inverse of the Jacobian of transformation. In Maxima we might do something like

  J : zeromatrix(3,3);
  for j : 1 thru 3 do (
    for i : 1 thru 3 do (
      J[i,j] : ’diff(indep[j],curvi[i])
    )
  );
  K : zeromatrix(3,3);
  for j : 1 thru 3 do (
    for i : 1 thru 3 do (
      K[i,j] : diff(curvi[j], indep[i])
    )
  );
  grid_trans_subs : matrixmap(”=”, K, invert(J));
  /* making substitutions from a list is easier than from a matrix */
  grid_trans_sublis : flatten(makelist(grid_trans_subs[i],i,1,3));

which gives us a list of nine equations we can use to make substitutions so that all our derivatives are with respect to the computational coordinates.

  trans_eqn : subst(grid_trans_sublis, eqn) $
  /* Evaluation took 0.0510 seconds (0.0553 elapsed) using 265.164 KB. */
  trans_eqn_factor : factor(trans_eqn) $
  /* Evaluation took 2.4486 seconds (2.5040 elapsed) using 48.777 MB. */

Factoring the result starts getting on up there in compute time and memory, but still not untractable, or even that uncomfortable for an interactive session. Of course we still haven’t made any difference expression substitutions, and that will expand the number of terms even further. The assumption that the grid is arbitrary is a decision point that would have to be dealt with in a black-box style implementation. Best to leave it to the (hopefully) knowledgeable user.

As an aside, linearization is another example of an assumption that is probably best left to the user. Wirth assumes that a linearization is required to solve nonlinear PDEs, whereas Cook provides for calculating the system Jacobians needed for Newton methods (of course Wirth does note that this is just one approach that could be used, and the tools are flexible enough to be extended to other methods). Using the Jacobian is a more modern approach made practical by the successful development of Newton-Krylov methods. It is impossible to predict the future development of numerical methods that will change the choices that need to be made in discretizing PDEs (though that doesn’t prevent speculation [14]), so a flexible toolbox approach is again indicated.

Once a PDE is defined substitutions of finite differences for partial derivatives must be made to create the discrete approximation. Wirth uses a function called DISCRETIZE which uses the dependencies list (created by a call to depends) to substitute indexed variables for the independent variables. Then the partial derivatives of the indexed variables are replaced by finite difference operators. The substitutions of difference expressions is controlled by using Maxima’s pattern matching rules. The basic recipe is

1. Define dependencies between independent and dependent (and possibly computational coordinates)
2. Associate a list if indices with the coordinates
3. Define rules that transform differential terms into difference terms with the appropriate index shifts and constant multipliers corresponding to the coordinate which the derivative is with respect to and the selected finite difference expression
4. Apply the rules to the PDE to give a finite difference equation (FDE)
5. Use Maxima’s simplification and factoring capabilities to simplify the FDE
6. Output the FDE in FORTRAN format and wrap with subroutine boilerplate using text processing macros

The boilerplate is a set of standard templates for a particular solution procedure. The example Wirth uses is an alternating direction implicit (ADI) scheme. A more modern example might be a Newton-Krylov scheme. Wirth describes an environment, Fast FORTRAN Programing (FFP), whose goal is to move computational physics out of a “cottage industry” state. He describes it thusly, “The system consists of two major components: a subroutine library and a command language for building, compiling and running codes.” Based on my experience, that sounds a whole lot like Scipy, which is built on top of Python, and packages together many of the classic scientific computing libraries.

Pattern matching in Maxima is relatively straight-forward. For instance, say I have a function that I’d like to use to calculate my derivatives (such as one based on the discrete cosine transform (DCT)), I could declare patterns that replaced derivatives with function calls.

  matchdeclare([fmatch,xmatch,nmatch],all),
  defrule(deriv_subst_1, ’diff(fmatch,xmatch,1), diff_1(fmatch,xmatch)),
  defrule(deriv_subst_2, ’diff(fmatch,xmatch,2), diff_2(fmatch,xmatch)),
  mat_expr : apply1(mat_expr, deriv_subst_1),
  mat_expr : apply1(mat_expr, deriv_subst_2),

This would result in all of the first and second derivatives in mat_expr being replaced by function calls diff_1 and diff_2 respectively.

The initial set-up steps Cook uses in [3] are roughly the same as those used by Wirth, with the addition of a constant list. The focus is more on what to do with the discrete expressions once they are generated. The basic recipe is

1. reduce_cnst()
2. gcfac()
3. optimize()
4. fortran()

The constant list allows reduce_cnst to pull constants out of loops, and optimize pulls out common sub-expressions to speed things up. optimize returns a Maxima block, which is similar to a Fortran subroutine. In fact, turning blocks into subroutines in other languages is a common problem which has been addressed on the Maxima mailing list (e.g. block2c, see also cform), and as Dan Stanger points out, this is the purpose of the GENTRAN package. GENTRAN is not yet successfully ported to work with Maxima [13] (though there is a gentran directory that ships in the Maxima source tarball if you want to take a look).

The only reason Cook went to the Lisp level in [3] was to reduce the cost of the factor routines (which is less of a concern now), and to make optimize work with lists of expressions (which it does now). One of the examples cites a need for an outrageous 500 million words of computer memory for one calculation, but that’s roughly half what’s in my old desktop computer I got used about a year ago (for about $100). The computing power available to the average amateur has come a long way since 1982.

Both Wirth and Cook assume that an arbitrary orthogonal coordinate system (like spherical, polar, cylindrical, Cartesian, etc.) will be defined. A slightly more modern approach is presented by Roache et al. [4, 5, 6]. They assume an arbitrary curvilinear coordinate system, which may not have analytical scale factors and metrics (i.e. they include the numerical grid generation task as part of the problem statement / solution procedure).

The approach demonstrated in [5] focuses on transforming a set of PDEs to arbitrary curvilinear coordinates described by Laplace’s equation. This approach couples the PDE solution and grid generation methods together. Modern approaches in the engineering world generally assume that the grid will be generated by a separate tool (the fully coupled approach can still be useful for adaptive or moving grids), though solving problems on a single, canonical grid seems to still be common in the sciences. The MACSYMA routines presented there are

change()

change variables, convert arbitrary second order differential equation in nn variables to an arbitrary coordinate frame in the variables xi[i]

notate

atomic notation for derivatives

notation(exp,vari)

primitive atomic notation

scheme()

introduce differences of unknowns

difference(u,f,exp)

primitive differences, scheme and difference collect the coefficients of the differences and calculate the stencil of the solver and coordinate transformations

myFORTRAN()

write the FORTRAN code

A lot of this extra effort is avoidable now, because it is tractable to use Maxima’s knowledge of the chain rule, and the built-in indexed variables and pattern matching facilities.

Conclusion

After digging in to the old literature on generating code from MACSYMA, and trying out a few things with current (v5.20.1) Maxima, it seems like all the pieces you need to generate PDE solving code already ship with Maxima (not touched on in this post were the vector calculus and tensor capabilities that Maxima has as well). I kind of already knew this since I'd been generating solver code in an ad hoc sort of way already. Perhaps there is a place for building up a pattern matching rules database, and maybe boilerplate templates. That seems to be the area that the modern efforts are focused on (e.g. Scinapse claims that it’s rules encoding PDE solution knowledge make up half it’s 120kloc and is the fastest growing part of the code-base [9]). The recipes presented here seem more like a documentation, or tutorial item rather than a possible new Maxima package.

References

[1]   Wirth, M. C., On the Automation of Computational Physics, Ph.D. thesis, University of California, Davis, 1980.

[2]   Wirth, M. C., “Automatic generation of finite difference equations and fourier stability analyses,” SYMSAC ’81: Proceedings of the fourth ACM symposium on Symbolic and algebraic computation, ACM, New York, NY, USA, 1981, pp. 73–78.

[3]   Cook, G. O., Development of a Magnetohydrodynamic Code for Axisymmetric, High-β Plasmas with Complex Magnetic Fields, Ph.D. thesis, Brigham Young University, December 1982.

[4]   Florence, M., Steinberg, S., and Roache, P., “Generating subroutine codes with MACSYMA,” Mathematical and Computer Modelling, Vol. 11, 1988, pp. 1107 – 1111.

[5]   Steinberg, S. and Roache, P. J., “Symbolic manipulation and computational fluid dynamics,” Journal of Computational Physics, Vol. 57, No. 2, 1985, pp. 251 – 284.

[6]   Steinber, S. and Roache, P., “Using VAXIMA to Write FORTRAN Code,” Applications of Computer Algebra, edited by R. Pavelle, Kulwer Academic Publishers, August 1984, pp. 74–94.

[7]   Cook, G. O., “Construction of large-scale simulation codes using ALPAL (A Livermore Physics Applications Language),” Technical Report UCRL-102469, Lawrence Livermore National Labs, October 1990.

[8]   Husa, S., Hinder, I., and Lechner, C., “Kranc: a Mathematica package to generate numerical codes for tensorial evolution equations,” Computer Physics Communications, Vol. 174, No. 12, 2006, pp. 983 – 1004.

[9]   Akers, R. L., Kant, E., Randall, C. J., Steinberg, S., and Young, R. L., Enabling Technologies for Computational Science, Vol. 548 of The Springer International Series in Engineering and Computer Science, chap. SCINAPSE: A problem solving environment for partial differential equations, Springer, 2000, pp. 109–122.

[10]   Hamming, R. W., “One Man’s View of Computer Science,” Journal of the Association for Computing Machinery, Vol. 16, No. 1, January 1969, pp. 3–12.

[11]   Cook, G. O., electronic mail communication, August 2010.

[12]   Fateman, R. J., electronic mail communication, August 2010.

[13]   Stanger, D., electronic mail communication, August 2010.

[14]   Houstis, E. N. and Rice, J. R., “Future problem solving environments for computational science,” Mathematics and Computers in Simulation, Vol. 54, No. 4-5, 2000, pp. 243 – 257.

Uncertainty Quantification with Stochastic Collocation

I’ve been posting lots of links to uncertainty quantification (UQ) references lately in comments (eg here, here, here), but I don’t really have a post dedicated only to UQ. So I figured I’d remedy that situaton. This post will be a simple example problem based on methods presented in some useful recent papers on UQ (along with a little twist of my own):

• A good overview of several of the related UQ methods [1]
• Discussion of some of the sampling approaches for high dimensional random spaces, along with specifics about the method for CFD [2]
• Comparison of speed-up over naive Monte Carlo sampling approaches [3]
• A worked example of stochastic collocation for a simple ocean model [4]

The example will be based on a nonlinear function of a single variable

(1)

The first step is to define a probability distribution for our input (Gaussian in this case, shown in Figure 1).

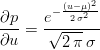(2)

---

Figure 1: Uncertain Input Distribution

---

Then, since our example is a simple function, we can analytically calculate the resulting probability density for the output. To do that we need the derivative of the model with respect to the input (in the multi-variate case we’d need the Jacobian).

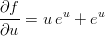(3)

Then we divide the input density by the slope to get the new output density.

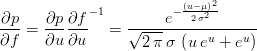(4)

We’ll use equation 4 to measure the convergence of our collocation method.

The idea of stochastic collocation methods is that the points which the model (equation 1 in our example) is evaluated at are chosen so that they are orthogonal with the probability distributions on the inputs as a weighting function. For normally distributed inputs this results in choosing points at the roots of the Hermite polynomials. Luckily, Scipy has a nice set of special functions, which includes he_roots to give us the roots of the Hermite polynomials. What we really want is not the function evaluation at the collocation points, but the slope at the collocation points. One way to get this information in a nearly non-intrusive way is to use a complex step method (this is that little twist I mentioned). So, once we have values for this slope at the collocation points we fit a polynomial to those points and use this polynomial as a surrogate for equation 3. Figure 2 shows the results for several orders of surrogate slopes.

---

Figure 2: Stochastic Collocation Estimates of Output Uncertainty

---

The convergence of the method is shown in Figure 3. For low dimensional random spaces (only a few random inputs) this method will be much more efficient than random sampling. Eventually the curse of dimensionality takes its toll though, and random sampling becomes the faster approach.

---

Figure 3: Convergence of the Collocation Method

---

The cool thing about this method is that the complex step method which I used to estimate the Jacobian is also useful for sensitivity quantification which can be used for design optimization as well. On a related note, Dan Hughes has a post describing an interesting approach to bounding uncertainties in the output of a calculation given bounds on the inputs by using interval arithmetic.

References

[1]   Loeven, G.J.A., Witteveen, J.A.S., Bijl, H., Probabilistic Collocation: An Efficient Non-Intrusive Approach For Arbitrarily Distributed Parametric Uncertainties, 45th Aerospace Sciences Meeting, Reno, NV, 2007.

[2]   Hosder, S., Walters, R.W., Non-Intrusive Polynomial Chaos Methods for Uncertainty Quantification in Fluid Dynamics, 48th Aerospace Sciences Meeting, Orlando, FL, 2010.

[3]   Xiu, D., Fast Numerical Methods for Stochastic Computations, Comm. Comp. Phys., 2009.

[4]   Webster, M., Tatang, M.A., McRae, G.J., Application of the Probabilistic Collocation Method for an Uncertainty Analysis of a Simple Ocean Model, MIT JPSPGC Report 4, 2000.

A Few Nits About Ensembles and Decision Support

First off, thanks to Steve Easterbrook for pointing at a new report on ensemble climate predictions. This post is some of my thoughts on that report.

Here's an interesting snippet from the first section of the report:

Within the last decade the causal link between increasing concentrations of anthropogenic greenhouse gases in the atmosphere and the observed changes in temperature has been scientifically established.

From a nice little summary of how to establish causation:

C. Establishing causation: The best method for establishing causation is an experiment, but many times that is not ethically or practically possible (e.g., smoking and cancer, education and earnings). The main strategy for learning about causation when we can’t do an experiment is to consider all lurking variables you can think of and look at how Y is associated with X when the lurking variables are held “fixed.”

D. Criteria for establishing causation without an experiment: The following criteria make causation more credible when we cannot do an experiment.

(i) The association is strong.

(ii) The association is consistent.

(iii) Higher doses are associated with stronger responses.

(iv) The alleged cause precedes the effect in time.

(v) The alleged cause is plausible.

The point being, if you can't do experiments, the causal link you establish will always be a rather contingent one (and if your population of 'lurkers' is only 4 or 5 then perhaps we aren't to the point of exhausting our imaginations yet).  I say that not to be disingenuous and sow doubt unnecessarily, but merely to show that I have an honest place to stand in my skepticism (I'd like to head off the "you're a willfully ignorant pseudo-scientific jerk" sorts of flames that seem to be popular in discussions on this topic).

That little digression aside, the specific aim of the work is to

develop an ensemble prediction system for climate change based on the principal state-of-the-art, high-resolution, global and regional Earth system models developed in Europe, validated against quality-controlled, high-resolution gridded datasets for Europe, to produce for the first time an objective probabilistic estimate of uncertainty in future climate at the seasonal to decadal and longer time-scales;

A side-note on climate alarmism: If the quality of the body of knowledge was such that it demanded action NOW! Then this would not have been the first such study. Rational decision support requires these sorts of uncertainty quantification efforts, it is totally irresponsible to demand political action without them.

The improvements for example, add skill to seasonal forecasting while multi-decadal models, for the first time, have produced probabilistic climate change projections for Europe.

Again, now that these projections have been made for the first time, we could actually attempt to validate them. I use that term in the technical sense of comparing a model's predictions to innovative experimental results. Since we can't do experiments on the earth (or can we?) we have to settle for either not validating, or validating by comparing the predictions to what actually happens. I realize that would take a couple decades to make useful quantitative comparisons. But think about this, if we've already bought a millenia of warming then can't we spend a decade or two to build the credibility in our tool-set which we'll be using to 'fly' the climate into the future for centuries to come? The fact that this set of ensemble results claims to be skillfull at the decadal time-scales would actually make the validation task a quicker one than it would be with less accurate models because you've taken some of the 'noise' and explained it with your model.

I got really excited about this, it sounds promising:

The multi-model ensemble builds on the experience of previous projects where it has been shown to be a successful method to improve the skill of seasonal forecasts from individual models. The perturbed parameter approach reflects uncertainty in physical model parameters, while the newly developed stochastic physics methodology represents uncertainty due to inherent errors in model parameterisations and to the unavoidably finite resolution of the models.

Then I got to this:

These results illustrate that initialised decadal forecasts have the potential to provide improved information compared with traditional climate change projections, but the optimal strategy for building improved decadal prediction systems in the presence of model biases remains an open question for future work.

Which reflects my impression of the state of the art from my little mini-lit review on Bayes Model Averaging. That's the fundamental difficulty, isn't it?

This is the sort of thing that worries folks who are used to being able to draw a bright line between calibration and validation:

The ENSEMBLES gridded observation data set was used along with other datasets to verify and calibrate both global and regional models, and also to assess the uncertainties in model response to anthropogenic forcing.

Recall Kelvin,

Conditional PDFs, which encompass the sampled uncertainty, were constructed from the statistically and dynamically downscaled output (and from GCM output) for temperature and/or precipitation for a number of areas and points. These are, however, qualitative constructions.

There's still some work to do here to make the product more useful for decision makers (quantitative rather than qualitative). I think the polynomial chaos expansion approaches being explored in the uncertainty quantification community have a lot of promise here (3 or 4 orders of magnitude speed-up over standard Monte Carlo approaches). The other slight difficulty with this approach is that these qualitative PDFs were then used as inputs into the impact assessments.

In light of the previous ensembles post and linked discussion thread, I found this snippet interesting:

The non-linear nature of the climate system makes dynamical climate forecasts sensitive to uncertainty in both the initial state and the model used for their formulation. Uncertainties in the initial conditions are accounted for by generating an ensemble from slightly different atmospheric and ocean analyses. Uncertainty in model formulation arises due to the inability of dynamical models of climate to simulate every single aspect of the climate system with arbitrary detail. Climate models have limited spatial and temporal resolution, so that physical processes that are active at smaller scales (e.g., convection, orographic wave drag, cloud physics, mixing) must be parameterised using semi-empirical relationships.

In that Adventures Among Alarmists post I made a sort of hand-wavy claim of everything about forecasting (from data assimilation on through to predictive distributions) being one big ill-posed problem with noise. I think reading section 3 of this report will give you a flavor of what I mean. One minor quibble: hindcasts are an ok sort of 'sanity' check, but we should take care to remember their dangers, and not mistake them for true validation. Taking too much confidence from hind-casts is a recipe for fooling ourselves.

The ensemble's skill changes with lead-time:

The skill increases for longer lead times, being larger for 6–10 years ahead than for 3–14 months or 2–5 years ahead. This is because the forced climate change signal, the sign of which is highly predictable, is greater at longer lead times.

This squares with the results discussed over here about BMA in climate and weather forecasting. Depending on the time-frame at which you are looking to forecast, different model weightings, and spin-up times are optimal. This also goes to the problem about the past-performance / future-skill connection. Since the feedbacks are not stationary, models which performed well in the past won't tend to perform well in the future (eg. the BMA weighting changes through time).

Encouragingly, the multi-model ensemble mean, which consists of the average of twelve individual projections, gives somewhat higher scores than any of the individual models, whose projections are derived from three members with perturbed initial conditions.

So, truth-centered or not?

The results also show that the skill increases for more recent hindcasts. In order to diagnose sources of skill, the blue curve of Figure 3.6 shows ensemble mean results from a parallel ensemble of ‘NoAssim’ hindcasts containing the same external forcing from greenhouse gases, sulphate aerosols, volcanoes and solar variations, but initialised from randomly selected model states rather than analyses of observations.

This seems like a reasonable use of hindcasts. Look for insight into the reasons particular models / realizations might have performed well on certain historical periods. They also found that initialization matters even with climate predictions (though their randomly selected initializations were pretty darn skill-full).

The product, decision support:

For many grid boxes there are significant probabilities of both drier and wetter future climates, and this may be important for impacts studies.

I think as regional projections start becoming more and more available, the extreme, alarmist policy prescriptions will be less and less well supported by a rational cost-benefit analysis.

The sensitivity study discussed in the report (done by climateprediction.net) is worth noting simply for the fact that they found an interesting interaction (that's always a fun part of experimentation). Some of the criticism of this effort has focused on the plausibility of some of the parameter combinations in the thousands of runs of this computer experiment. The distinction to keep in mind is that this is a sensitivity study rather than a complete uncertainty quantification study.

Well it said in the executive summary that they generated 'qualitative PDFs', but it seems like section 3.3.2 is describing a quantitative Bayesian approach. They sample their parameter space with a variety of models with varying levels of complexity and then fit a simple surrogate (some people might call it a response surface) so that they can get approximate 'results' for the whole space. Then they get posterior probabilities by weighting expert obtained priors by likelihoods, a straight-forward application of Bayes Theorem. That seems as quantitative as anyone could ask for, maybe I'm missing something?

They give a nice summary of the different types of uncertainties:

Also, the three techniques for sampling modelling uncertainty are essentially complementary to one another, so should not be seen as competing alternatives: the multi-model approach samples structural variations in model formulation, but does not systematically explore parameter uncertainties for a given set of structural choices, whereas the perturbed parameter approach does the reverse. The stochastic physics approach recognises the uncertainty inherent in inferring the effects of parameterised processes from grid box average variables which cannot account for unresolved sub-grid-scale organisations in the modelled flow, whereas the other methods do not. There is likely to be scope to develop better prediction systems in future by combining aspects of the separate systems considered in ENSEMBLES.

I think section 3 was the meat of the report (at least for what I'm interested in), so I'll stop with the commentary on that report there. I want to end with an answer to the question often suggested for dealing with us ornery skeptics, "What evidence would it take to convince you?" This is usually meant to be a jab, because obviously skeptics are really deniers in disguise and we couldn't possibly be reasonable or consider evidence (and it also displays one of the common fallacies of regarding disagreement about policy with ignorance of science, science demands nothing but a method). My answer is a simple one: Rational policy tied to skillful prediction. By rational policy I mean it is foolish to focus on the cost-benefit of extreme events far out into the future weighed against mitigation today or tomorrow (because the tails of those future cost distributions are so uncertain, and the immediate costs of mitigation are relatively well known). It is far more rational to look at the near-term cost-benefit of adaption to climate changes (no matter their cause) and evolutionary improvements to our irrigation, flood management, public health and energy diversity problems. The skillfulness of near-term predictions can be reasonably validated, and then used to guide policy. This should be a natural extension of the way we already make agriculture and infrastructure decisions based on weather predictions and an understanding of our current climate. There's no need for the slashing and burning of evil western capitalism (or whatever the rallying cry at Copenhagen was). The ability to skillfully predict changes further and further into the future can be gradually validated (by making a prediction and then waiting, sorry that's what seems reasonable to me) and then the results of those tools can be incorporated into policy decisions. Markets and people don't respond well to shocks. Gradualism may not be sexy, but it's smart.