|
| This Ain't New Mexico |
Monday, January 31, 2011
Sunday, January 23, 2011
Better Recurrence Plots
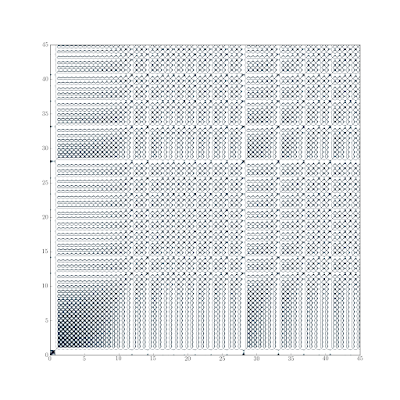
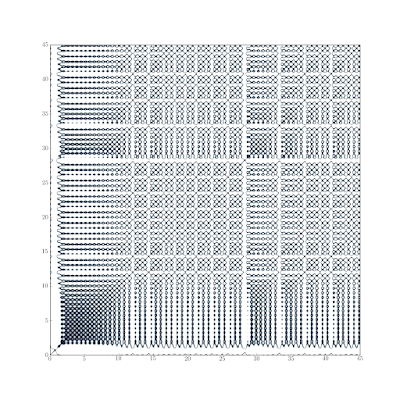
In the previous post in the Lorenz63 series we used recurrence plots to get a qualitative feel for the type of behavior exhibited by a time series (stochastic, periodic, chaotic). Those were using the default colormap in matplotlib, and they seem to highlight the “holes” more than the “near returns” (at least to my eye). Here’s some improved ones that use the bone colormap and a threshold on the distance to better highlight the near returns.
Saturday, January 22, 2011
Recurrence, Averaging and Predictability
Motivation and Background
Yet another installment in the Lorenz63 series. This time motivated by a commenter on Climate Etc. Tomas Milanovic claims that time averages are chaotic too in response to the oft repeated claim that the predictability limitations of nonlinear dynamical systems are not a problem in the case of climate prediction. Lorenz would seem to agree, “most climatic elements, and certainly climatic means, are not predictable in the first sense at infinite range, since a non-periodic series cannot be made periodic through averaging [1].” We’re not going to just take his word on it. We’ll see if we can demonstrate this with our toy model.
That’s the motivation, but before we get to toy model results a little background discussion is in order. In this previous entry I illustrated the different types of functionals that you might be interested in depending on whether you are doing weather prediction or climate prediction. I also made the remark, “A climate prediction is trying to provide a predictive distribution of a time-averaged atmospheric state which is (hopefully) independent of time far enough into the future.” It was pointed out to me that this is a testable hypothesis [2], and that the empirical evidence doesn’t seem to support the existence of time-averages (or other functionals) describing the Earth’s climate system that are independent of time [3]. In fact, the above assumption was critiqued by none other than Lorenz in 1968 [4]. In that paper he states,
Questions concerning the existence and uniqueness of long-term statistics fall into the realm of ergodic theory. [...] In the case of nonlinear equations, the uniqueness of long-term statistics is not assured. From the way in which the problem is formulated, the system of equations, expressed in deterministic form, together with a specified set of initial conditions, determines a time-dependent solution extending indefinitely into the future, and therefore determines a set of long-term statistics. The question remains as to whether such statistics are independent of the choice of initial conditions.
He goes on to define a system as transitive if the long-term statistics are independent of initial condition, and intransitive if there are “two or more sets of long-term statistics, each of which has a greater-than-zero probability of resulting from randomly chosen initial conditions.” Since the concept of climate change has no meaning for statistics over infinitely long intervals, he then defines a system as almost intransitive if the statistics at infinity are unique, but the statistics over finite intervals depend (perhaps even sensitively) on initial conditions. In the context of policy relevance we are generally interested in behavior over finite time-intervals.
In fact, from what I’ve been able to find, different large-scale spatial averages (or coherent structures, which you could track by suitable projections or filtering) of state for the climate system face similar limits to predictability as un-averaged states. The predictability just decays at a slower rate. So instead of predictive limitations for weather-like functionals on the order of a few weeks, the more climate-like functionals become unpredictable on slower time-scales. There’s no magic here, things don’t suddenly become predictable a couple decades or a century hence because you take an average. It’s just that averaging or filtering may change the rate that errors for that functional grow (because in spatio-temporal chaos different structures, or state vectors, will have different error growth rates and reach saturation at different times). Again Lorenz puts it well, “the theory which assures us of ultimate decay of atmospheric predictability says nothing about the rate of decay” [1]. Recent work shows that initialization matters for decadal prediction, and that the predictability of various functionals decay at different rates [5]. For instance, sea surface temperature anomalies are predictable at longer forecast horizons than surface temperatures over land. Hind-casts of large spatial averages on decadal time-scales have shown skill in the last two decades of the past century (though they had trouble beating a persistence forecast for much of the rest of the century) [6].
I’ve noticed in on-line discussions about climate science that some people think that the problem of establishing long term statistics for nonlinear systems is a solved one. That is not the case for the complex, nonlinear systems we are generally most interested in (there are results for our toy though [7, 8]). I think this snippet sums things up well,
Atmospheric and oceanic forcings are strongest at global equilibrium scales of 107 m and seasons to millennia. Fluid mixing and dissipation occur at micorscales of 10-3 m and 10-3s, and cloud particulate transformations happen at 10-6 m or smaller. Observed intrinsic variability is spectrally broad band across all intermediate scales. A full representation for all dynamical degrees of freedom in different quantities and scales is uncomputable even with optimistically foreseeable computer technology. No fundamentally reliable reduction of the size of the AOS [atmospheric oceanic simulation] dynamical system (i.e., a statistical mechanics analogous to the transition between molecular kinetics and fluid dynamics) is yet envisioned. [9]
Here McWilliams is making a point similar to that made by Lorenz in [4] about establishing a statistical mechanics for climate. This would be great if it happened, because that would mean that the problem of turbulence would be solved for us engineers too. Right now the best we have (engineers interested in turbulent flows and climate scientists too) is empirically adequate models that are calibrated to work well in specific corners of reality.
Lorenz was responsible for another useful concept concerning predictability, that is predictability of the first and second kind [1]. If you care about the time-accurate evolution of the order of states then you are interested in predictability of the first kind. If, however, you do not care about the order, but only the statistics, then you are concerned with predictability of the second kind. Unfortunately, Lorenz’s concepts of first and second kind predictability have been morphed in to a claim that first kind predictability is about solving initial value problem (IVP)s and second kind predictability is about solving boundary value problem (BVP)s. For example, “Predictability of the second kind focuses on the boundary value problem: how predictable changes in the boundary conditions that affect climate can provide predictive power [5].” This is unsound. If you read Lorenz closely, you’ll see that the important open question he was exploring about whether the climate is transitive, intransitive or almost intransitive has been assumed away by the spurious association of kinds of predictability with kinds of problems [1]. Lorenz never made this mistake, he was always clear that the difference in kinds of predictability depends on the functionals you are interested in, not whether it is appropriate to solve an IVP or a BVP (what reason could you have for expecting meaningful frequency statistics from a solution to a BVP?). Those considerations depend on the sort of system you have. In an intransitive or almost intransitive system even climate-like functionals depend on the initial conditions.
A good early paper on applying information theory concepts to climate predictability is by Leung and North [10], and there is a more recent review article that covers the basic concepts by DelSole and Tippett [11].
Recurrence Plots
Recurrence plots are useful for getting a quick qualitative feel for the type of response exhibited by a time-series [12, 13]. First we run a little initial condition (IC) ensemble with our toy model. The computer experiment we’ll run to explore this question will consist of perturbations to the initial conditions (I chose the size of the perturbation so the ensemble would blow-up around t = 12). Rather than sampling from a distribution for the members of the ensemble, I chose them according a stochastic collocation (this helps in getting the same results every time too).
One thing that these two plots makes clear is that it doesn’t make much sense to compare individual trajectories with the ensemble mean. The mean is a parameter of a distribution describing a population of which the trajectories are members. While the trajectories are all orbits on the attractor, the mean is not.
Comparing the chaotic recurrence plots with the plots below of a periodic series and a stochastic series illustrates the qualitative differences in appearance.
Clearly, both the ensemble mean and the individual trajectory are chaotic series, sort of “between” periodic and stochastic in their appearance. Ensemble averaging doesn’t make our chaotic series non-chaotic, what about time averaging?
Predictability Decay
How does averaging affect the decay of predictability for the state of the Lorenz63 system, and can we measure this effect? We can track how the predictability of the future state decays given knowledge of the initial state by using the relative entropy. There are other choices for measures such as mutual information [10]. Since we’ve already got our ensemble though, we can just use entropy like we did before. Rather than just a simple moving average, I’ll be calculating an exponentially weighted one using an FFT-based approach, of course (there’s some edge effects we’d need to worry about if this were a serious analysis, but we’ll ignore that for now). The entropy for the ensemble is shown for three different smoothing levels in Figure 4 (the high entropy prior to t = 5 for the smoothed series is spurious because I didn’t pad the series and it’s calculated with the FFT).
While smoothing does lower the entropy of the ensemble (lower entropy for more smoothing / smaller λ), it still experiences the same sort of “blow-up” as the unsmoothed trajectory. This indicates problems for predictability even for our time-averaged functionals. Guess what? The recurrence plot indicates that our smoothed trajectory is still chaotic!
This result shouldn't be too surprising, moving averages or smoothing (of whatever type you fancy) are linear operations. It would probably take a pretty clever nonlinear transformation to turn a chaotic series into a non-chaotic one (think about how the series in this case is generated in the first place). I wouldn't expect any combination of linear transformations to accomplish that.
Conclusions
I’ll begin the end with another great point from McWilliams (though I’ve not heard of sub-grid fluctuations referred to as “computational noise,” that term makes me think of round-off error) that should serve to temper our demands of predictive capability from climate models[9]:
Among their other roles, parametrizations regularize the solutions on the grid scale by limiting fine-scale variance (also known as computational noise). This practice makes the choices of discrete algorithms quite influential on the results, and it removes the simulation from the mathematically preferable realm of asymptotic convergence with resolution, in which the results are independent of resolution and all well conceived algorithms yield the same answer.
If I had read this earlier, I wouldn’t have spent so much time searching for something that doesn’t exist.
Regardless of my tortured learning process, what do the toy models tell us? Our ability to predict the future is fundamentally limited. Not really an earth-shattering discovery; it seems a whole lot like common sense. Does this have any implication for how we make decisions? I think it does. Our choices should be robust with respect to these inescapable limitations. In engineering we look for broad optimums that are insensitive to design or requirements uncertainties. The same sort of design thinking applies to strategic decision making or policy design. The fundamental truism for us to remember in trying to make good decisions under the uncertainty caused by practical and theoretical constraints is that limits on predictability do not imply impotence.
References
[1] Lorenz, E. N., The Physical Basis of Climate and Climate Modeling, Vol. 16 of GARP publication series, chap. Climatic Predictability, World Meteorological Organization, 1975, pp. 132–136.
[2] Pielke Sr, R. A., “your query,” September 2010, electronic mail to the author.
[3] Rial, J. A., Pielke Sr, R. A., Beniston, M., Claussen, M., Canadell, J., Cox, P., Held, H., Noblet-Ducoudr, N. D., Prinn, R., Reynolds, J. F., and Salas, J. D., “Nonlinearities, Feedbacks And Critical Thresholds Within The EarthS Climate System,” Climatic Change, Vol. 65, No. 1-2, 2004, pp. 11–38.
[4] Lorenz, E. N., “Climatic Determinism,” Meteorological Monographs, Vol. 8, No. 30, 1968.
[5] Collins, M. and Allen, M. R., “Assessing The Relative Roles Of Initial And Boundary Conditions In Interannual To Decadal Climate Predictability,” Journal ofClimate, Vol. 15, No. 21, 2002, pp. 3104–3109.
[6] Lee, T. C., Zwiers, F. W., Zhang, X., and Tsao, M., “Evidence of Decadal Climate Prediction Skill Resulting from Changes in Anthropogenic Forcing,” Journal of Climate, Vol. 19, 2006.
[7] Tucker, W., The Lorenz Attractor Exists, Ph.D. thesis, Uppsala University, 1998.
[8] Kehlet, B. and Logg, A., “Long-Time Computability of the Lorenz System,”http://lorenzsystem.net/.
[9] McWilliams, J. C., “Irreducible Imprecision In Atmospheric And Oceanic Simulations,” Vol. 104 of National Academy of Sciences, National Academy of Sciences, pp. 8709 – 8713.
[10] Leung, L.-Y. and North, G. R., “Information Theory and Climate Prediction,”Journal of Climate, Vol. 3, 1990, pp. 5–14.
[11] DelSole, T. and Tippett, M. K., “Predictability: Recent insights from information theory,” Reviews of Geophysics, Vol. 45, 2007.
[12] Eckmann, J.-P., Kamphorst, S. O., and Ruelle, D., “Recurrence Plots of Dynamical Systems,” EPL (Europhysics Letters), Vol. 4, No. 9, 1987, pp. 973.
[13] Marwan, N., “A historical review of recurrence plots,” The European PhysicalJournal - Special Topics, Vol. 164, 2008, pp. 3–12, 10.1140/epjst/e2008-00829-1.
Wednesday, January 19, 2011
Empiricism and Simulation
There are two orthogonal ideas that seem to get conflated in discussions about climate modeling. One is the idea that you’re not doing science if you can’t do a controlled experiment, but of course we have observational sciences like astronomy. The other is that all this new-fangled computer-based simulation is untrustworthy, usually because “it ain’t the way my grandaddy did science.” Both are rather silly ideas. We can still weigh the evidence for competing models based on observation, and we can still find protection from fooling ourselves even when those models are complex.
What does it mean to be an experimental as opposed to an observational science? Do sensitivity studies, and observational diagnostics using sophisticated simulations count as experiments? Easterbrook claims that because climate scientists do these two things with their models that climate science is an experimental science [1]. It seems like there is a motivation to claim the mantle of experimental, because it may carry more rhetorical credibility than the merely observational (the critic Easterbrook is addressing certainly thinks so). This is probably because the statements we can make about causality and the strength of the inferences we can draw are usually greater when we can run controlled experiments than when we are stuck with whatever natural experiments fortune provisions for us (and there are sound mathematical reasons for this, having to do with optimality in experimental design rather than any label we may place on the source of the data). This seeming motivation demonstrated by Easterbrook to embrace the label of empirical is in sharp contrast to the denigration of the empirical by Tobis in his three part series [2, 3, 4]. As I noted on his site, the narrative Tobis is trying to create with those posts has already been pre-messed with by Easterbrook, his readers just pointed out the obvious weaknesses too. One good thing about blogging is the critical and timely feedback.
The confusions of these two climate warriors are an interesting point of departure. I think they are both saying more than blah blah blah, so it’s worth trying to clarify this issue. The figure below is based on a technical report from Sandia [5], which is a good overview and description of the concepts and definitions for model verification and validation as it has developed in the computational physics community over the past decade or so. I think this emerging body of work on model V&V places the relative parts, experiment and simulation, in a sound framework for decision making and reasoning about what models mean.
|
The process starts at the top of the flowchart with a “Reality of Interest”, from which a conceptual model is developed. At this point the path splits into two main branches. One based on “Physical Modeling” and the other based on “Mathematical Modeling”. Something I don’t think many people realize is that there is a significant tradition of modeling in science that isn’t based on equations. It is no coincidence that an aeronautical engineer might talk of testing ideas with a wind-tunnel model or a CFD model. Both models are simplifications of the reality of interest, which, for that engineer, is usually a full-scale vehicle in free flight.
Figure 2 is just a look at the V&V process through my Design of Experiments (DoE) colored glasses.
My distorted view of the V&V process is shown to emphasize that there’s plenty of room for experimentalists to have fun (maybe even a job [3]) in this, admittedly model-centric, sandbox. However, the transferability of the basic experimental design skills between “Validation Experiments” and “Computational Experiments” says nothing about what category of science one is practicing. The method of developing models may very well be empirical (and I think Professor Easterbrook and I would agree it is, and maybe even should be), but that changes nothing about the source of the data which is used for “Model Validation.”
The computational experiments highlighted in Figure 2 are for correctness checking, but those aren’t the sorts of computational experiments Easterbrook claimed made climate science an experimental science. Where do sensitivity studies and model-based diagnostics fit on the flowchart? I think sensitivity studies fit well in the activity called “Pre-test Calculations”, which, one would hope, inform the design of experimental campaigns. Diagnostics are more complicated.
Heald and Wharton have a good explanation for the use of the term “diagnostic” in their book on microwave-based plasma diagnostics: “The term ‘diagnostics,’ of course, comes from the medical profession. The word was first borrowed by scientists engaged in testing nuclear explosions about 15 years ago [c. 1950] to describe measurements in which they deduced the progress of various physical processes from the observable external symptoms” [6]. With a diagnostic we are using the model to help us generate our “Experimental Data”, so that would happen within the activity of “Experimentation” on this flowchart. This use of models as diagnostic tools is applied to data obtained from either experiment (e.g. laboratory plasma diagnostics) or observations (e.g. astronomy, climate science), so it says nothing about whether a particular science is observational or experimental. Classifying scientific activities as experimental or observational is of passing interest, but I think far too much emphasis is placed on this question for the purpose of winning rhetorical “points.”
The more interesting issue from a V&V perspective is introducing a new connection in the flowchart that shows how a dependency between model and experimental data could exist (Figure 3). Most of the time the diagnostic model, and the model being validated are different. However, this case where they are the same is an interesting and practically relevant one that is not addressed in the current V&V literature that I know of (please share links if you “know of”).
It should be noted that even though the same model may be used to make predictions and perform diagnostics, it will usually be run in a different way for those two uses. The significant changes between Figure 1 and Figure 3 are the addition of a “Experimental Diagnostic” box and the change to the mathematical cartoon in the “Validation Experiment” box. The change to the cartoon is to indicate that we can’t measure what we want directly (u), so we have to use a diagnostic model to estimate it based on the things we can measure (b). An example of when the model-based diagnostic is relatively independent of the model being validated might be using laser-based diagnostic for fluid flow. The equations describing propagation of the laser through the fluid are not the same as those describing the flow. An example of when the two codes might be connected would be if you were trying to use ultrasound to diagnose a flow. The diagnostic model and the predictive model could both be Navier-Stokes with turbulence closures. Establishing the validity of which is the aim of the investigation. I’d be interested in criticisms of how I explained this / charted this out.
Afterward
Attempt at Answering Model Questions
I’m not in the target population that professor Easterbrook is studying, but here’s my attempt at answering his questions about model validation[7].
- “If I understand correctly–a model is ’valid’ (is that a formal term?) if the code is written to correctly represent the best theoretical science at the time...”
I think you are using an STS flavored definition for “valid.” The IEEE/AIAA/ASME/US-DoE/US-DoD definition differs. “Valid” means observables you get out of your simulations are “close enough” to observables in the wild (experimental results). The folks from DoE tend to argue for a broader definition of valid than the DoD folks. They’d like to include as “validation” activities of a scientist comparing simulation results and experimental results without reference to an intended use.
- “– so then what do the results tell you? What are you modeling for–or what are the possible results or output of the model?”
Doing a simulation (running the implementation of a model) makes explicit the knowledge implicit in your modeling choices. The model is just the governing equations, you have to run a simulation to find solutions to those governing equations.
- “If the model tells you something you weren’t expecting, does that mean it’s invalid? When would you get a result or output that conflicts with theory and then assess whether the theory needs to be reconsidered?”
This question doesn’t make sense to me. How could you get a model output that conflicted with theory? The model is based on theory. Maybe this question is about how simplifying assumptions could lead to spurious results? For example, if a simulation result shows failure to conserve mass/momentum/energy in a specific calculation possibly due to a modeling assumption (more likely due to a more mundane error), I don’t think anyone but a perpetual-motion machine nutter would seriously reconsider the conservation laws.
- “Then is it the theory and not the model that is the best tool for understanding what will happen in the future? Is the best we can say about what will happen that we have a theory that adheres to what we know about the field and that makes sense based on that knowledge?”
This one doesn’t make sense to me either. You have a “theory,” but you can’t formulate a “model” of it and run a simulation, or just a pencil and paper calculation? I don’t think I’m understanding how you are using those words.
- “What then is the protection or assurance that the theory is accurate? How can one ‘check’ predictions without simply waiting to see if they come true or not come true?”
There’s no magic; the protection from fooling ourselves is the same as it has always been, only the names of the problems change.
Attempt at Understanding Blah Blah Blah
- “The trouble comes when empiricism is combined with a hypothesis that the climate is stationary, which is implicit in how many of their analyses work.” [8]
The irony of this statement is extraordinary in light of all the criticisms by the auditors and others of statistical methods in climate science. It would be a valid criticism, if it were supported.
- “The empiricist view has never entirely faded from climatology, as, I think, we see from Curry. But it’s essentially useless in examining climate change. Under its precepts, the only thing that is predictable is stasis. Once things start changing, empirical science closes the books and goes home. At that point you need to bring some physics into your reasoning.” [2]
So we’ve gone from what could be reasonable criticism of unfounded assumptions of stationarity to empiricism being unable to explain or understand dynamics. I guess the guys working on embedding dimension stuff, or analogy based predictions would be interested to know that.
- “See, empiricism lacks consilience. When the science moves in a particular direction, they have nothing to offer. They can only read their tea leaves. Empiricists live in a world which is all correlation, and no causation.” [3]
Lets try some definitions.
- empiricism
- knowledge through observation
- consilience
- unity of knowledge, non-contradiction
How can the observations contradict each other? Maybe a particular explanation for a set of observations is not consilient with another explanation for a different set of observations. This seems to be something that would get straightened out in short order though: it’s on this frontier that scientific work proceeds. I’m not sure how empiricism is “all correlation.” This is just a bald assertion with no support.
- “While empiricism is an insufficient model for science, while not everything reduces to statistics, empiricism offers cover for a certain kind of pseudo-scientific denialism. [...] This is Watts Up technique asea; the measurements are uncertain; therefore they might as well not exist; therefore there is no cause for concern!” [4]
Tobis: Empiricism is an insufficient model for science. Feynman: The test of all knowledge is experiment. Tobis: Not everything reduces to statistics. Jaynes: Probability theory is the logic of science. To be fair, Feynman does go on to say that you need imagination to think up things to test in your experiments, but I’m not sure that isn’t included in empiricism. Maybe it isn’t included in the empiricism Tobis is talking about.
So that’s what all this is about? You’re upset at Watts making a fallacious argument about uncertainty? What does empiricism have to do with this? It would be simple enough to just point out that uncertainty doesn’t mean ignorance.
Not quite blah blah blah, but the argument is still hardly thought out and poorly supported.
References
[1] Easterbrook, S., “Climate Science is an Experimental Science,”http://www.easterbrook.ca/steve/?p=1322, February 2010.
[2] Tobis, M., “The Empiricist Fallacy,” http://initforthegold.blogspot.com/2010/11/empiricist-fallacy.html, November 2010.
[3] Tobis, M., “Empiricism as a Job,”http://initforthegold.blogspot.com/2010/11/empiricism-as-job.html, November 2010.
[4] Tobis, M., “Pseudo-Empiricism and Denialism,”http://initforthegold.blogspot.com/2010/11/pseudo-empiricism-and-denialism.html, November 2010.
[5] Thacker, B. H., Doebling, S. W., Hemez, F. M., Anderson, M. C., Pepin, J. E., and Rodriguez, E. A., “Concepts of Model Verification and Validation,” Tech. Rep. LA-14167-MS, Los Alamos National Laboratory, Oct 2004.
[6] Heald, M. and Wharton, C., Plasma Diagnostics with Microwaves, Wiley series in plasma physics, Wiley, New York, 1965.
[7] Easterbrook, S., “Validating Climate Models,”http://www.easterbrook.ca/steve/?p=2032, November 2010.
[8] Tobis, M., “Empiricism,”http://initforthegold.blogspot.com/2010/11/empiricism.html, November 2010.
Thanks to George Crews and Dan Hughes for their critical feedback on portions of this.
[Update: George left a comment with suggestions on changing the flowchart. Here's my take on his suggested changes.
A slightly modified version of George's chart. I think it makes more sense to have the "No" branch of the validation decision point back at "Abstraction", which parallels the "No" branch of the verification decision pointing at "Implementation". Also switched around "Experimental Data" and "Experimental Diagnostic." Notably absent is any loop for "Calibration"; this would properly be a separate loop with output feeding in to "Computer Model." ]Saturday, January 8, 2011
Mathematical Science Foundations of Validation, Verification, and Uncertainty Quantification
- A committee of the NRC will examine practices for verification and validation (V&V) and uncertainty quantification (UQ) of large-scale computational simulations in several research communities.
- Identify common concepts, terms, approaches, tools, and best practices of V&V and UQ.
- Identify mathematical sciences research needed to establish a foundation for building a science of V&V and for improving practice of V&V and UQ.
- Recommend educational changes needed in the mathematical sciences community and mathematical sciences education needed by other scientific communities to most effectively use V&V and UQ.
Here's a list of the folks on the committee. It should be interesting to see the study results (it's an 18 month long effort).