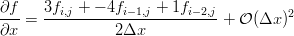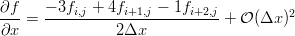NALPAL: Not A Livermore Physics Applications Language

Background and Motivation

The problem I am interested in: leverage high-level symbol manipulation capabilities in a computer algebra system (CAS) to generate compile-able code for number crunching. More specifically, I am interested in generating routines for numerical partial differential equation (PDE) solvers. This is not a new idea, significant work was accomplished starting in the early 1980s [1, 2, 3], continued into the late ’80s [4, 5, 6], and early ’90s [7]. However, those capabilities have not been consolidated and formally incorporated into my open-source CAS of choice, Maxima (though there is fairly recent work implementing similar ideas for Mathematica [8, 9]). The early work [1] quotes Hamming’s Turing Award speech [10] for motivation:

We seem not to be able to use the machine, which we all believe is a very powerful tool for manipulating and transforming information, to do our own tasks in this very field. We have compilers, assemblers, monitors, etc. for others, and yet when I examine what the typical software person does, I am often appalled at how little he uses the machine in his own work.

I had been thinking about this problem for a while because of my interest in method of manufactured solutions (MMS) for code verification. I thought things were really going to take off when I came across Cook’s 1990 technical report describing code generation for PDE solvers using A Livermore Physics Applications Language (ALPAL), which was built on top of DOE-MACSYSMA. ALPAL aimed to be a general purpose domain specific language for turning symbolic descriptions of PDEs into code. Here’s a solution to the problem already developed! Of course, it couldn’t be that easy. I asked the Maxima mailing list if anyone knew what became of this effort: ALPAL question to Maxima list, and ended up answering my own question by getting a hold of some of the old ALPAL devs: ALPAL answer to the list. Unfortunately, there is a long history behind the divergence between different versions of MACSYMA (and different groups of developers) that mitigates against this old code ever working with the fork that became Maxima (should an archive of the source ever actually turn up, update: it did, see comment) [11, 12, 13].

As you may have guessed from this post’s title, and the difficulties described in the previous paragraph, I’ve decided to pursue a more toolbox approach rather than (re)implementing a domain specific language and associated decision logic. The working title for my toolbox of utilities will be NALPAL, both as a nod to the valuable historical work in this area, and an indication of the path not taken.

Wirth categorizes three main approaches to systems for numerical PDE solution: black-box systems, subroutine packages, and code generation aids [1]. Black-box systems are intended for the novice user, and tend to be constrained to very specific problem types or incorporate a great deal of decision logic. Subroutine packages provide reusable building blocks, but require more knowledge and coding on the part of the user, and tend to remain problem specific. Code generation aids require the user to be an expert in numerical analysis, and tend not to automate any of the analytical work that precedes the code generation step.

Wirth’s suggested approach is a Unix-like toolbox approach where standard subroutine libraries are used when it makes sense to do so, and utilities for doing custom code generation are written in the CAS environment. The alternative is to create a full language, and incorporate the semantics and decision logic to automate the entire process for the novice user. The work of Wirth, Steinberg and Roache is a good example of the former approach, and Cook’s work on ALPAL is an example of the latter (though his early work [3] is more along the lines of the toolbox approach, going so far as to say “the viewpoint taken is that one should be able to start with integro-differential equations and end up with optimal FORTRAN code segments. The key in achieving this goal was to tackle only the specific algebraic problem-i at hand, and not to attempt to provide tools to cover every conceivable numerical scheme.”). The toolbox approach keeps more of the work for the problem solver in set-up/tear-down/customization, while the language approach loads more of the burden on to the domain specific language developer. Wirth’s second objective sums up well the approach that I think makes the most sense (emphasis original):

Build productivity enhancing tools of broad applicability for the expert user so that efficient, special purpose PDE codes can be built reliably and quickly, rather than attempt to second guess the expert and build general purpose PDE codes (black box systems) of doubtful efficiency and reliability.

There are still useful things to learn from ALPAL even if we have chosen the less ambitious road, since the problem being solved is the same. A basic description of the ALPAL use-case [7]:

1. Take as input a PDE description, along with boundary and initial condition definitions
2. Discretize the PDE
3. Analyze the result (e.g. for stability)
4. Calculate the Jacobian (needed for Newton methods in implicit time-integration or non-linear boundary value problem (BVP)s)
5. Generate code

Even if we don’t have a full-featured language, the user of our set of utilities will still be interested in accomplishing largely these same steps. In fact, Wirth’s early work gives these steps (reproduced here verbatim) [1]:

1. Manipulate the set of partial differential equations to cast them into a form that is amenable to numerical solution. For vector PDEs, this might include vector differential calculus operations and reexpression in scalar (component) form, and the application of a linearization approximation for non-linear PDEs.
2. Discretize the time and space domain, and transform the partial differential operators in the PDEs into finite difference operators. This transforms the partial differential equations into a set of algebraic equations. A multitude of possible transformations for the differential operators are possible and the boundary conditions for the PDEs also must be appropriately handled. The resulting difference equations must be analyzed to see if they form an accurate and numerically stable approximation of the original equation set. For real world problems, this analysis is usually difficult and often intractable.
3. After choosing a solution algorithm from numerical linear algebra, the finite difference equations and boundary conditions are coded in a programing language such as FORTRAN.
4. The numerical algorithm is then integrated with code for file manipulations, operating system interactions, graphics output, etc. forming a complete computer program.
5. The production program is then executed, and its output is analyzed, either in the form of numerical listings or computer-generated graphics.

Wirth goes on to say (emphasis added),

With continuing advances in computer technology, the last step in this process has become easier. For a given class of problems, answers can be calculated more quickly and economically. More importantly, harder problems which require more computational resources can be solved. But the first four steps have not yet benefited from advances in computer performance; in fact, they are aggravated by it.

Also, this additional bit of motivation from Chapter 5,

Taken together with the software described in other chapters, these tools allow the user to quickly generate a FORTRAN code, run numerical experiments, and discard the code without remorse if the numerical results are unsatisfactory.

This is similar in sentiment to the idea of numerical throw away code.

PDE Code Gen Recipes

With the problem background and motivation set, the rest of this post will focus on pulling out useful Maxima recipes demonstrated by folks who have generated FORTRAN from MACSYMA with intent to inflict grievous arithmurgical damage on hapless PDEs.

Much work is done in most of these articles from the 1980s to avoid array references and break up expressions by hand to reduce the computational cost in MACSYMA. Also, MACSYMA’s knowledge of the chain rule is not used for calculating the transformations because of an explosion in the number of terms [5], rather an identity for the derivative of a matrix inverse is used. A lot of this effort seems unnecessary today because speed and memory have improved so much. However, the basic approach and variables used to define the problem is still relevant (compare with this example of Burgers’ equation on a curvilinear grid):

  dep : [f, sigma]; /* the dependent variables */
  curvi : [xi, eta, zeta]; /* the curvilinear coordinates */
  indep : [x, y, z]; /* the independent variables */
  depends(curvi, indep);
  depends(dep, curvi);
  nn : length(indep);
  eqn : sum(diff(sigma * diff(f, indep[i]), indep[i]), i, 1, nn);

The result is rather large, but it illustrates Maxima’s knowledge of the chain rule. Of course, generally it is easiest to compute rather than for an arbitrary grid, so you need to make substitutions based on the inverse of the Jacobian of transformation. In Maxima we might do something like

  J : zeromatrix(3,3);
  for j : 1 thru 3 do (
    for i : 1 thru 3 do (
      J[i,j] : ’diff(indep[j],curvi[i])
    )
  );
  K : zeromatrix(3,3);
  for j : 1 thru 3 do (
    for i : 1 thru 3 do (
      K[i,j] : diff(curvi[j], indep[i])
    )
  );
  grid_trans_subs : matrixmap(”=”, K, invert(J));
  /* making substitutions from a list is easier than from a matrix */
  grid_trans_sublis : flatten(makelist(grid_trans_subs[i],i,1,3));

which gives us a list of nine equations we can use to make substitutions so that all our derivatives are with respect to the computational coordinates.

  trans_eqn : subst(grid_trans_sublis, eqn) $
  /* Evaluation took 0.0510 seconds (0.0553 elapsed) using 265.164 KB. */
  trans_eqn_factor : factor(trans_eqn) $
  /* Evaluation took 2.4486 seconds (2.5040 elapsed) using 48.777 MB. */

Factoring the result starts getting on up there in compute time and memory, but still not untractable, or even that uncomfortable for an interactive session. Of course we still haven’t made any difference expression substitutions, and that will expand the number of terms even further. The assumption that the grid is arbitrary is a decision point that would have to be dealt with in a black-box style implementation. Best to leave it to the (hopefully) knowledgeable user.

As an aside, linearization is another example of an assumption that is probably best left to the user. Wirth assumes that a linearization is required to solve nonlinear PDEs, whereas Cook provides for calculating the system Jacobians needed for Newton methods (of course Wirth does note that this is just one approach that could be used, and the tools are flexible enough to be extended to other methods). Using the Jacobian is a more modern approach made practical by the successful development of Newton-Krylov methods. It is impossible to predict the future development of numerical methods that will change the choices that need to be made in discretizing PDEs (though that doesn’t prevent speculation [14]), so a flexible toolbox approach is again indicated.

Once a PDE is defined substitutions of finite differences for partial derivatives must be made to create the discrete approximation. Wirth uses a function called DISCRETIZE which uses the dependencies list (created by a call to depends) to substitute indexed variables for the independent variables. Then the partial derivatives of the indexed variables are replaced by finite difference operators. The substitutions of difference expressions is controlled by using Maxima’s pattern matching rules. The basic recipe is

1. Define dependencies between independent and dependent (and possibly computational coordinates)
2. Associate a list if indices with the coordinates
3. Define rules that transform differential terms into difference terms with the appropriate index shifts and constant multipliers corresponding to the coordinate which the derivative is with respect to and the selected finite difference expression
4. Apply the rules to the PDE to give a finite difference equation (FDE)
5. Use Maxima’s simplification and factoring capabilities to simplify the FDE
6. Output the FDE in FORTRAN format and wrap with subroutine boilerplate using text processing macros

The boilerplate is a set of standard templates for a particular solution procedure. The example Wirth uses is an alternating direction implicit (ADI) scheme. A more modern example might be a Newton-Krylov scheme. Wirth describes an environment, Fast FORTRAN Programing (FFP), whose goal is to move computational physics out of a “cottage industry” state. He describes it thusly, “The system consists of two major components: a subroutine library and a command language for building, compiling and running codes.” Based on my experience, that sounds a whole lot like Scipy, which is built on top of Python, and packages together many of the classic scientific computing libraries.

Pattern matching in Maxima is relatively straight-forward. For instance, say I have a function that I’d like to use to calculate my derivatives (such as one based on the discrete cosine transform (DCT)), I could declare patterns that replaced derivatives with function calls.

  matchdeclare([fmatch,xmatch,nmatch],all),
  defrule(deriv_subst_1, ’diff(fmatch,xmatch,1), diff_1(fmatch,xmatch)),
  defrule(deriv_subst_2, ’diff(fmatch,xmatch,2), diff_2(fmatch,xmatch)),
  mat_expr : apply1(mat_expr, deriv_subst_1),
  mat_expr : apply1(mat_expr, deriv_subst_2),

This would result in all of the first and second derivatives in mat_expr being replaced by function calls diff_1 and diff_2 respectively.

The initial set-up steps Cook uses in [3] are roughly the same as those used by Wirth, with the addition of a constant list. The focus is more on what to do with the discrete expressions once they are generated. The basic recipe is

1. reduce_cnst()
2. gcfac()
3. optimize()
4. fortran()

The constant list allows reduce_cnst to pull constants out of loops, and optimize pulls out common sub-expressions to speed things up. optimize returns a Maxima block, which is similar to a Fortran subroutine. In fact, turning blocks into subroutines in other languages is a common problem which has been addressed on the Maxima mailing list (e.g. block2c, see also cform), and as Dan Stanger points out, this is the purpose of the GENTRAN package. GENTRAN is not yet successfully ported to work with Maxima [13] (though there is a gentran directory that ships in the Maxima source tarball if you want to take a look).

The only reason Cook went to the Lisp level in [3] was to reduce the cost of the factor routines (which is less of a concern now), and to make optimize work with lists of expressions (which it does now). One of the examples cites a need for an outrageous 500 million words of computer memory for one calculation, but that’s roughly half what’s in my old desktop computer I got used about a year ago (for about $100). The computing power available to the average amateur has come a long way since 1982.

Both Wirth and Cook assume that an arbitrary orthogonal coordinate system (like spherical, polar, cylindrical, Cartesian, etc.) will be defined. A slightly more modern approach is presented by Roache et al. [4, 5, 6]. They assume an arbitrary curvilinear coordinate system, which may not have analytical scale factors and metrics (i.e. they include the numerical grid generation task as part of the problem statement / solution procedure).

The approach demonstrated in [5] focuses on transforming a set of PDEs to arbitrary curvilinear coordinates described by Laplace’s equation. This approach couples the PDE solution and grid generation methods together. Modern approaches in the engineering world generally assume that the grid will be generated by a separate tool (the fully coupled approach can still be useful for adaptive or moving grids), though solving problems on a single, canonical grid seems to still be common in the sciences. The MACSYMA routines presented there are

change()

change variables, convert arbitrary second order differential equation in nn variables to an arbitrary coordinate frame in the variables xi[i]

notate

atomic notation for derivatives

notation(exp,vari)

primitive atomic notation

scheme()

introduce differences of unknowns

difference(u,f,exp)

primitive differences, scheme and difference collect the coefficients of the differences and calculate the stencil of the solver and coordinate transformations

myFORTRAN()

write the FORTRAN code

A lot of this extra effort is avoidable now, because it is tractable to use Maxima’s knowledge of the chain rule, and the built-in indexed variables and pattern matching facilities.

Conclusion

After digging in to the old literature on generating code from MACSYMA, and trying out a few things with current (v5.20.1) Maxima, it seems like all the pieces you need to generate PDE solving code already ship with Maxima (not touched on in this post were the vector calculus and tensor capabilities that Maxima has as well). I kind of already knew this since I'd been generating solver code in an ad hoc sort of way already. Perhaps there is a place for building up a pattern matching rules database, and maybe boilerplate templates. That seems to be the area that the modern efforts are focused on (e.g. Scinapse claims that it’s rules encoding PDE solution knowledge make up half it’s 120kloc and is the fastest growing part of the code-base [9]). The recipes presented here seem more like a documentation, or tutorial item rather than a possible new Maxima package.

References

[1]   Wirth, M. C., On the Automation of Computational Physics, Ph.D. thesis, University of California, Davis, 1980.

[2]   Wirth, M. C., “Automatic generation of finite difference equations and fourier stability analyses,” SYMSAC ’81: Proceedings of the fourth ACM symposium on Symbolic and algebraic computation, ACM, New York, NY, USA, 1981, pp. 73–78.

[3]   Cook, G. O., Development of a Magnetohydrodynamic Code for Axisymmetric, High-β Plasmas with Complex Magnetic Fields, Ph.D. thesis, Brigham Young University, December 1982.

[4]   Florence, M., Steinberg, S., and Roache, P., “Generating subroutine codes with MACSYMA,” Mathematical and Computer Modelling, Vol. 11, 1988, pp. 1107 – 1111.

[5]   Steinberg, S. and Roache, P. J., “Symbolic manipulation and computational fluid dynamics,” Journal of Computational Physics, Vol. 57, No. 2, 1985, pp. 251 – 284.

[6]   Steinber, S. and Roache, P., “Using VAXIMA to Write FORTRAN Code,” Applications of Computer Algebra, edited by R. Pavelle, Kulwer Academic Publishers, August 1984, pp. 74–94.

[7]   Cook, G. O., “Construction of large-scale simulation codes using ALPAL (A Livermore Physics Applications Language),” Technical Report UCRL-102469, Lawrence Livermore National Labs, October 1990.

[8]   Husa, S., Hinder, I., and Lechner, C., “Kranc: a Mathematica package to generate numerical codes for tensorial evolution equations,” Computer Physics Communications, Vol. 174, No. 12, 2006, pp. 983 – 1004.

[9]   Akers, R. L., Kant, E., Randall, C. J., Steinberg, S., and Young, R. L., Enabling Technologies for Computational Science, Vol. 548 of The Springer International Series in Engineering and Computer Science, chap. SCINAPSE: A problem solving environment for partial differential equations, Springer, 2000, pp. 109–122.

[10]   Hamming, R. W., “One Man’s View of Computer Science,” Journal of the Association for Computing Machinery, Vol. 16, No. 1, January 1969, pp. 3–12.

[11]   Cook, G. O., electronic mail communication, August 2010.

[12]   Fateman, R. J., electronic mail communication, August 2010.

[13]   Stanger, D., electronic mail communication, August 2010.

[14]   Houstis, E. N. and Rice, J. R., “Future problem solving environments for computational science,” Mathematics and Computers in Simulation, Vol. 54, No. 4-5, 2000, pp. 243 – 257.

Derivative of Unequally Spaced Points

I posted a while back on solving Burgers' equation on a moving grid. The same coordinate transformation techniques applied there can be used to calculate the derivative of unequally spaced data points. Just as in the moving grid application, the grid transformation takes the points in the physical space to the computational space. Once in computational space, the sky's the limit!

One way to do this would be just a simple, low-order finite difference for the first derivative, maybe using an average of two one-sided differences (that would reduce to a central difference if the points were equally spaced). We can easily do better than that though since there are so many great, optimized transforms available in the FFTW library. Spectral methods give results that are accurate down to the precision of the machine for more than about 20 points (for functions without discontinuities).

The cost of using a grid-transformation is that we have to calculate two derivatives and then multiply them together, and the cost of a spectral method is O(n*log(n)) instead of O(n) as in a finite difference approximation. In one-dimension things are pretty easy, the chain rule shows us the two derivatives we need to calculate:

It is not straight-forward to directly calculate the additional derivative, so we calculate it by inverting the derivative of the physical coordinate with respect to the computational one:

Using the discrete cosine transform from FFTW (Chebyshev psuedospectral method) is straightforward to do by using F2Py and Python:

n = 17 # number of data points
a = 0.0 # left side of the interval
b = 3 * np.pi # right side of the interval
alpha = 0.25 # parameter to scale the perturbation
dx = (b - a) / float(n) # this is the equally spaced delta x
half_interval = (b - a) / 2.0 # so the dct diff is properly normalized
n_perturb = 3 # number of perturbed sets to try

dx_perturb = alpha * dx * (sp.random.random_sample((n,n_perturb)) - 0.5)

x = np.linspace(a, b, n)
dxdxi_perturb = np.zeros((n,n_perturb),dtype=float)
dydxi_perturb = np.zeros((n,n_perturb),dtype=float)
y_perturb = np.zeros((n,n_perturb),dtype=float)
x_perturb = np.zeros((n,n_perturb),dtype=float)

for i in xrange(n_perturb):
x_perturb[:,i] = x + dx_perturb[:,i] # add in the random fluctuations

y = np.cos(x)
y_perturb = np.cos(x_perturb)
dxdxi = cs.dct_diff(x, half_interval)
dy_analytical = - np.sin(x)
dydxi = cs.dct_diff(y, half_interval)
# derivatives with respect to the computational coordinate:
for i in xrange(n_perturb):
dxdxi_perturb[:,i] = cs.dct_diff(x_perturb[:,i], half_interval)
dydxi_perturb[:,i] = cs.dct_diff(y_perturb[:,i], half_interval)

# now actually calculate the derivatives we're after:
dydx = dydxi / dxdxi
dydx_perturb = dydxi_perturb / dxdxi_perturb

The derivative of the physical coordinate with respect to the computational coordinate for the equally spaced case and a couple of cases with some random perturbations added:

The actual derivative that we're after:

This example shows the flexibility of the approach, but it also indicates the importance of smooth changes in grid spacing for accurate derivative approximations. Abrupt changes in grid spacing translates into noise in the derivative.

FFTW Discrete Cosine Transform Derivative

I've done several posts lately about finite difference methods. Spectral methods are the ultimate extension of these same basic ideas used from Boole on up to the present. For an interesting read on this progression (or lack thereof) check out the preface of Boyd's spectral methods book.

Instead of using a series of overlapping local derivative expressions, the derivative at each point is calculated with an interpolating polynomial that spans the entire grid. This leads to exponential (rather than the usual first, second, etc) order of convergence. For folks used to finite differences, Fornberg has written a concise guide that focuses especially on the connection between finite difference approximations and pseudospectral methods.

There are a couple of things that make spectral methods practical for a wide variety of engineering problems (not just periodic boundaries). The most important being Chebyshev Polynomials, which through a little change of variables can be calculated with Fourier transforms, or discrete cosine transform (DCT) for a factor of four speed-up over the FFT. Luckily the excellent FFTW library has specialized transforms for real, even data which we can use to calculate our DCTs with nice, optimized O(n*log(n)) algorithms for arbitrary length data. Here is a thread discussing the usage of FFTW's DCT for calculating derivatives.

Chebyshev polynomial in terms of cos():

From the FFTW docs the forward and inverse discrete cosine transforms (DCTs) are


Notice the similarity between the Chebyshev polynomial and the formula for the coefficients of the DCT.

Here's a Fortran routine that uses the DCT Type II and Type III from FFTW to calculate the derivative of a non-periodic function. An important thing to do when using spectral methods on non-periodic functions is to choose grid points that are at the roots of the Chebyshev polynomials. This makes them equally spaced in the angular coordinate, so we can use the standard transform libraries (which expect equally spaced data). Choosing nodes this way also helps with Runge's Phenomenon.

subroutine dct_diff(dydx, y, half_interval, n)
! use the discrete cosine transform from fftw to calculate the derivative
integer, intent(in) :: n ! number of data points
double precision, intent(in), dimension(n) :: y ! function values
double precision, intent(out), dimension(n) :: dydx ! derivative values
double precision, intent(in) :: half_interval ! half the interval length
double precision, dimension(n) :: beta ! derivative coefficients
double precision, dimension(n) :: alpha ! function coefficients
integer :: plan1, plan2, i
integer :: n_logical ! the logical size of the transform, size of
! the corresponding real symmetric DFT

! the logical size depends on the type of transform, check the docs:
! http://www.fftw.org/doc/1d-Real_002deven-DFTs-_0028DCTs_0029.html
n_logical = 2*(n)

! forward DCT:
call dfftw_plan_r2r_1d(plan1, n, y, alpha, FFTW_REDFT10, FFTW_ESTIMATE)
call dfftw_execute_r2r(plan1, y, alpha)
call dfftw_destroy_plan(plan1)
alpha = alpha / half_interval

! recurrence for the derivative coefficients:
beta(n) = 0D0
beta(n-1) = 2D0 * dble(n-1) * alpha(n)
do i = n-1, 2, -1
beta(i-1) = beta(i+1) + 2D0 * dble(i-1) * alpha(i)
end do
beta = - beta ! this makes it work, but not sure why!

! inverse DCT:
call dfftw_plan_r2r_1d(plan2, n, beta, dydx, FFTW_REDFT01, FFTW_ESTIMATE)
call dfftw_execute_r2r(plan2, beta, dydx)
call dfftw_destroy_plan(plan2)

! FFTW computes the un-normalized transforms, normalize by logical size
dydx = dydx / dble(n_logical)

end subroutine dct_diff

I compile this with F2Py so I can use all the nice facilities of Numpy and Scipy. Here's a Python convenience function for giving nodes based on the Chebyshev roots:

def arb_int_opt_nodes(a,b,n): # function to give Chebyshev points on an interval
y = numpy.zeros(n)
for i in xrange(n):
y[n-i-1] = numpy.cos( (2*i + 1)*numpy.pi/(2*n) )
return(((b - a) * y + b + a) / 2.0)

Try it out on a test function:

with a known analytical derivative:

The test function and its derivative using six grid points:

Convergence graph:

Pretty awesome, down to the round-off plateau with less than 20 points on the interval. This recent book on Chebyshev polynomials has a good tabulated example of integrating and differentiating a Chebyshev series on pp 33 - 35 that was very useful in debugging.

Perhaps a more practically useful test function is one-wavelength of cos(). This will give us an idea of how many nodes per wavelength we need for high accuracy solutions.


Which looks to give a rule of thumb of about twenty nodes per wavelength to get down to the round-off plateau (32 bit double precision).

Scroll back up and take a look at the Fortran again, see that sign change after the recurrence? Know why it's there? Leave a comment and let me know if you think you do.

Three Dimensional Poisson's Equation

This is a follow up to the post I wrote a while back about implementing numerical methods. The goal is to demonstrate a work-flow using tools that come included in the Fedora Linux (and many other) distributions.

1. In Maxima
   
   • Define governing equations
     
   • Substitute finite difference expressions for differential expressions in the governing equations
     
   • Output appropriate difference expressions to Fortran using f90()
     
2. In Fortran: wrap the expression generated by Maxima in appropriate functions, subroutines and modules
   
   
3. In Python
   
   • Compile modules with f2py, which comes packaged along with numpy
     
   • Write the high-level application code, parsing input decks, performing optimization, grid convergence studies, or visualizations that use the compiled Fortran modules
     

Maxima

The governing equation is the three-dimensional Poisson's equation. In Cartesian coordinates The Maxima code to define this equation is straightforward:

depends(u,x); depends(u,y); depends(u,z); /* Poisson's equation: */ p : 'diff(u,x,2) + 'diff(u,y,2) + 'diff(u,z,2) = -f;

Now that we have the continuous differential equation defined we can decide on what sort of discrete approximation we are going to solve. The simple thing to do with second derivatives is to use central differences of second order accuracy, which require only information from closest neighbours in the finite difference grid. Replacing the differential expressions with difference expressions is accomplished in Maxima with the ratsubst() function.

/* substitue difference expressions for differential ones: */
p : ratsubst((u[i-1,j,k] - 2*u[i,j,k] + u[i+1,j,k])/dx**2 , 'diff(u,x,2), p);
p : ratsubst((u[i,j-1,k] - 2*u[i,j,k] + u[i,j+1,k])/dy**2 , 'diff(u,y,2), p);
p : ratsubst((u[i,j,k-1] - 2*u[i,j,k] + u[i,j,k+1])/dz**2 , 'diff(u,z,2), p);
/* substitute the correct array value of f:*/
p : ratsubst(f[i,j,k], f, p);

This assumes that the solution u and the forcing function f are stored in three dimensional arrays, if not then the indexing in the difference expressions becomes more complicated. If we want to apply a Gauss-Seidel method to solve our elliptic problem we just need to solve p for u[i,j,k], and then dump that expression to Fortran format.

gs : solve(p, u[i,j,k]);
del : part(gs[1],2) - u[i,j,k];
/* output for fortran: */
with_stdout("gs.f90", f90(d = expand(del)));

This gives the expression for the update to the solution at each iteration of the solver.

Fortran

The Maxima expressions developed above need control flow added so they get applied properly to our solution array.

do k = 1, nz
do j = 1, ny
do i = 1, nx
d = (dy**2*dz**2*u(i+1,j,k)+dx**2*dz**2*u(i,j+1,k)+dx**2*dy**2* & u(i,j,k+1)+dx**2*dy**2*dz**2*f(i,j,k)+dx**2*dy**2* & u(i,j,k-1)+dx**2*dz**2*u(i,j-1,k)+dy**2*dz**2*u(i-1,j,k))/ & ((2*dy**2+2*dx**2)*dz**2+2*dx**2*dy**2)-u(i,j,k) u(i,j,k) = u(i,j,k) + w*d
end do
end do
end do

The expression for the update was generated from our governing equations in Maxima, one of the things to notice is the w that multiplies our update, this is so we can do successive over relaxation. Also, we'll go ahead and package several of these iterative schemes into a Fortran module

module iter_schemes
implicit none
contains

...bunches of related subroutines and functions ...

end module iter_schemes

Python

Now we want to be able to call our Fortran solution schemes from Python. Using F2py makes this quite simple:

[command-line]$ f2py -m iter_schemes -c iter_schemes.f90

This should result in a python module iter_schemes.so that can be imported just as any other module.

import numpy
from iter_schemes import *

... do some cool stuff with our new module in Python ...

Conclusion

This approach might seem like over-kill for the fairly simple scalar equation we used, but think about the complicated update expressions that can be generated for large vector partial differential equations like the Navier-Stokes or Maxwell's equations. Having these expressions automatically generated and ready to be wrapped in loops can save lots of initial development and subsequent debugging time. It also makes generating unit tests easier, and so encourages good development practice. But does it work? Of course, here's the convergence of the Gauss-Seidel and SOR schemes discussed above along with a Jacobi scheme and a conjugate gradient scheme applied to a 50 by 50 by 50 grid with a manufactured solution. The plot was generated with the Python module matplotlib.

Treating Image Edges

There are some good examples floating around of creating customized image processing kernels in the python imaging library (PIL). It's very convenient to simply define your own mask, and the library takes care of the convolution.

One drawback is that the edges don't get filtered in this process. There are various ad-hoc things you can do. You can just drop a line of pixels all the way around the picture, so the gradient image of a 800x600 picture would be 798x598 pixels (if you're using a compact stencil), or you could just copy the edge pixels from the old picture to the new picture. So in effect, the edges don't get filtered. For most applications this is probably no big deal, but it might be, and we can do better.

All we have to do is change our difference operator for the edge pixels, use a forward or backward difference on the edges rather than the central differences used on the interior. Then you get gradient info for your edge pixels too!

Customizing the PIL kernel class has been done, so I'm going to use Fortran90 and F2Py for my difference operators. I'll still use the PIL for all of the convenient image reading/writing utilities though. No need to implement that in Fortran!

We can use our little Maxima script to generate the differences we need on the edges. If you've taken a basic numerical methods course you'll probably recognize them as the three point forward and backward difference approximations for the first derivative.



The Python to do just that is here:

import sys, math, Image, numpy
from filters import *


if __name__ == '__main__':
in_img = Image.open(sys.argv[1])
in_img = in_img.convert("L")
out_img = Image.new("L", in_img.size)
pix = in_img.getdata()
# put the pixels into a fortran contiguous array:
pix_array = numpy.array(pix)
pix_array = pix_array.reshape( in_img.size, order='F' )
# calculate the gradient
g = first_order_gradient(pix_array,in_img.size[0],in_img.size[1])
gmag = 255 - numpy.sqrt( g[0,:,:]*g[0,:,:] + g[1,:,:]*g[1,:,:] )
gmag.astype("int")
# pack the gradient magnitude into a new image
out_img.putdata( gmag.reshape( gmag.size, order='F' ) )
out_img.save(sys.argv[2])

Where I've used F2Py to generate the filters module from a Fortran90 file. The module defines the subroutine first_order_gradient(), which implements the ideas discussed above. The gradients on the interior points are calculated using a central difference:

! apply the central operator to the interior pixels
do j = 2, nj-1
do i = 2, ni-1
g(1,i,j) = (in_image(i+1,j) - in_image(i-1,j)) / 2.0
g(2,i,j) = (in_image(i,j+1) - in_image(i,j-1)) / 2.0
end do
end do

The gradients along the edges are calculated using the forward and backward differences (only x edges shown for brevity):

! loop over the y dimension and apply the asymmetric operators to the
! x min and x max edges
do j = 2, nj-1 ! leave out the corners
i = 1 ! minimum edge, go forward
g(1,i,j) = (-3.0*in_image(i,j) + 4.0*in_image(i+1,j) - in_image(i+2,j))/2.0
i = ni ! maximum edge, go backward
g(1,i,j) = (3.0*in_image(i,j) - 4.0*in_image(i-1,j) + in_image(i-2,j))/2.0
! no change for the y derivative
i = 1
g(2,i,j) = (in_image(i,j+1) - in_image(i,j-1)) / 2.0
i = ni
g(2,i,j) = (in_image(i,j+1) - in_image(i,j-1)) / 2.0
end do

Finally the four corners are calculated separately, because each one has a unique combination of stencils required. Putting the loops in Fortran speeds things up considerably compared to the pure Python implementations I did before. Here is the gradient magnitude of the dials from Poor Man's ADC calculated with the above technique:

Implementing Numerical Methods: an IDE (sort of)

What would an integrated development environment for numerical algorithms look like? To me it looks a lot like Fedora. That’s right, Fedora Linux is your integrated development environment. Oh, separate programs in an operating system isn't integrated enough for you? They ought to be, Python or Bash are right there waiting to glue it all together.

An implementer or developer of numerical methods ought to have a good computer algebra system(CAS) available. This is where the high-level algorithm design needs to take place. All the rest of the low level coding needs to be automated as much as possible. You as the human in the loop need to spend time thinking about the bigger picture and get Maxima to code Fortran for you.

Numerical software needs testing. Lots of rigorous testing. You can use your (CAS) to generate unit tests by evaluating the expressions you converted to Fortran for specific cases, and then converting these answers to Fortran too. Then you can easily wrap those routines in a unit testing framework using F2Py.

This approach lets you automate the generation of the low-level functions that will be in your inner loops (which need to be in Fortran for performance sake). Then use Python's powerful standard library and additional packages for things like parsing input decks, file reading and creation, setting up parallel jobs and generating graphics. All things which can be a real pain in Fortran. The real benefit is that the human effort is kept focused where it is most profitably employed: at the higher levels of abstraction of the mathematical concepts rather than the low level coding.

There it is, a complete "environment" in three building blocks: Maxima, Fortran and Python. Almost completely automated from governing equations in the CAS to low-level number crunching in Fortran. Some human intervention required to bring it all together into a working program, but that’ll be in Python, which is easy.

This is the basic method used in the second half of the magnetron problem. I'll post some more simple examples of the whole work-flow in use after the holidays.

Maxima Codes Fortran90 for Me

Maxima is great. In the magnetron post we integrated the differential equation describing an electron's motion in a couple of different ways. The implicit methods required a matrix inversion and then matrix-vector multiply for each time-step. Instead of writing out and coding the expressions describing that operation by hand (painful bugs quite likely, ouch!) it is much easier to let Maxima code the Fortran for us. If you have to ask "why Fortran?", then you are obviously some kind of quiche eating software weenie. If instead, you thought, "of course Fortran, what else would Maxima code?", please read on, you number crunching stud (or studette).

Start up a Maxima session (I run Fedora 9, but I'm sure most other distributions have it, I think they even have a windows installer). It's easy to define our matrix operator, invert it, and apply it:

L : matrix(
[1,0,0, -dt, 0, 0],
[0,1,0, 0, -dt, 0],
[0,0,1, 0, 0, -dt],
[0,0,0, 1, a*B[3]/c,-a*B[2]/c],
[0,0,0,-a*B[3]/c, 1, a*B[1]/c],
[0,0,0, a*B[2]/c,-a*B[1]/c, 1] );

Linv : invert(L);

X: [x,y,z,vx,vy,vz];
P : a*[0,0,0,E[1],E[2],E[3]];
RHS : X - P;

LinvRHS : factor( expand( Linv.RHS ) );


Simple as that we have a symbolic representation of our inverted operator acting on our state vector. Now we want Fortran90 expressions.

load("f90");

fname : "back_euler_inv_op.f90";
f : openw(fname);

printf( f, "! These fortran expressions generated automatically from
! the maxima batch file magnetron.mac ~%");

for i : 1 thru length(LinvRHS) do
( printf( f, "x_n1(~d)=",i),
with_stdout( f, f90(LinvRHS[i,1]) ) );

close(f);


There is a small bug in the "f90" module (as of version 5.15) that causes it to use the Fortran77 style continuation when writing out a matrix, so that is why each element must be written out with a separate call to f90().

Well, that's neat, but I need to appease the quiche eaters, so wouldn't it be better if these expressions, and our inner loops (the time integration loop for this case) in Fortran were callable from something flexible and trendy like Python? That's where F2Py comes in. Generating a module for Python is one simple call:

f2py -c back_euler_sub.f90 -m back_euler

Where my subroutine using the Maxima generated expressions is in the file "back_euler_sub.f90" and the module will be named "back_euler".

The python script to use our new module is quite short:

from numpy import *
from back_euler import *

B = zeros( 3 )
E = zeros( 3 )
x_n = zeros( 6 )
x_n1 = zeros( 6 )
q = -4.8032e-10
m = 9.1094e-28
c = 2.9979e10
dt = 3e-10
nt = 50
E[1] = -1.0/3.0
B[2] = 33.6412

X = zeros( (6,nt), dtype='double', order='F' )

X = back_euler(nt,dt,q,m,c,E,B)

Now our low-level number crunching and inner loop is in nice, fast compiled F90 and we can call it from a high-level, object-oriented language to do things like zero finding (as in the magnetron post), or optimization or something else entirely.