This post is another installment in the Lorenz63 series. In it I’ll try to address a common confusion among folks trying to understand what uncertainty in initial conditions means for our ability to predict the future state of a system (in particular as it pertains to climate change). The common pedagogical technique is to describe weather prediction as an initial value problem (IVP) and climate prediction as a boundary value problem (BVP) (for example see Serendipity). I don’t think that happens to be a very good teaching technique (it seems too hand-wavy to me [update: better reasoning given down in this comment and this comment]). I think there are probably better approaches which would give more insight into the problems. I’m a learn by doing / example kind of guy, so that’s what this post will focus on: using the Lorenz ’63 system as a useful toy to give insight into the problem.
In fact, predictions of both climate and weather often use the same models which approximately solve the same initial-boundary value problem described by partial differential equations (PDE)s for the conservation of mass, momentum and energy (along with many parametrizations for physical and chemical processes in the atmosphere as well as sub-grid scale models of unresolved flow features). The real distinction is that climate researchers and weather forecasters care about different functions or statistics of the solutions over different time-scales. A weather forecast depends on providing time-accurate predictive distributions of the state of the atmosphere in the near-future. A climate prediction is trying to provide a predictive distribution of a time-averaged atmospheric state which is (hopefully) independent of time far enough into the future (there’s an implicit ergodic hypothesis here, which, as reader Tom Vonk points out, still requires some theoretical developments to justify for the PDEs we’re actually interested in).
Another concept I’d like to introduce before I show example results from the Lorenz ’63 system is the entropy of a probability distribution. This can be viewed as a measure of informativeness of the distribution. [update: this paper presents the idea in context of climatic predictions] So a very informative distribution would have low entropy, but an uninformative distribution would have maximum entropy. For weather forecasting we would like low entropy in our predictive distributions, because that means we have significant information about what is going to happen. For climate, the distribution itself is what we want, and we are actually in some sense looking for the maximum entropy distribution that is consistent with our constraints. Measuring the “distance” between distributions with different constraints is what climate forecasting is all about.
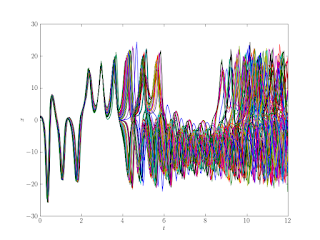
Now for the toying with the Lorenz63 system. The “ensembles” I’m running are just varying the initial condition in the x-component (using the same approach shown here). I’m also using two slightly different bx parameters in the forcing function. Figure 1 shows the x-component of the resulting trajectories.
The analogy to the weather / climate difference is pretty well illustrated by these results. Up to t ~ 3 we could do some pretty decent “weather” prediction, the ensemble members stay close together. After that things diverge abruptly (exponential growth in initial differences), this illustrates the need to “spin-up” a model when you are interested in the climate distributions. After t ~ 10 we could probably start estimating the “climate” of the two different forcings (histograms for 10 < t < 12 shown in Figure 2).
These trajectories illustrate another interesting aspect of deterministic chaos, our uncertainty in the future state does not increase monotonically, it will grow and shrink in time (for instance compare the spread in the ensemble members at t = 4 to that at t = 8 shown in Figure 1). The entropy in the distribution of the trajectories as a function of time is shown in Figure 3. A Python function to calculate this for my ensemble (stored in a 2d array) is shown below.
def ensemble_entropy(x):
# the ensemble runs accross the first dimension of x, the time
# runs accross the second, return entropy as a function of time
eps = 1e-16
ent = sp.zeros(x.shape[1], dtype=float)
bin_edges = sp.linspace(
min(x.ravel()), max(x.ravel()), int(sp.sqrt(x.shape[0])))
for i in xrange(x.shape[1]):
# the histogram function returns a probability density with normed=True
p = sp.histogram(x[:,i], bins=bin_edges, normed=True)
# we would like a probability mass for each bin, so we need to
# multiply by the width of the bin:
dx = p[1][1] - p[1][0]
p = dx * p[0]
# normalize (it’s generally very close, this is probably
# unnecessary), and take care of zero p bins so we don’t get
# NaNs in the log:
p = p / sum(p) + eps
ent[i] = -sum(p * sp.log(p))
return(ent)
The entropy gives us a nice measure of the informativeness of our ensemble. In the initial stages (t < 4) we’ve got small entropy (we could make “weather” predictions here). There’s a significant spike around t = 4, and then we see the magnitude of entropy drop off for a bit (or a nat, ha-ha) around t = 8, which matches the eye-balling of the ensemble spread we did earlier.
That’s it for toy model results, now for some conclusions and opinions.
There are two honest concerns with climate forecasting (if you know of more let me hear about them, if you don’t think my concerns are honest, let me hear that too). First, are the things we can predict with climate modeling useful for planing mitigation and adaption policies? So many of the alarming predictions of costs and catastrophes attributed to climate change in the press (and even in the IPCC’s reports) depend on particular regional (rather than global) climate changes. I think an open research question is how the time averaging (and large time-steps) involved in calculating the long trajectories for estimating equilibrium climate distributions (setting aside the theoretical underpinning of this ergodic assumption) affect the accuracy of the predicted spatial variations and regional changes (it is after-all a PDE rather than an ordinary differential equations (ODE)). This seems to be an area of research that is just beginning. Also, the papers I’ve been able to find so far don’t seem to report any grid convergence index results for the solutions (please link to papers that do have this in the comments if you know of any, thanks). This is an important part of what Roache calls calculation verification (as opposed to the code verification demonstrated here).
Second, what about the details of the ’averaging window’ (in both space and time)? How useful to policy are the results of long time-averages? Are the equilibrium distributions things we will ever actually reach? These two concerns about the usefulness of the climate modeling product for policy makers (and in a Republic like mine, the public), and the details about the averaging, seem to be the motivation for Pielke Sr.’s quibble over in this thread about the definition of climate and the implications of chaos. As Pielke points out, take your averaging volume small enough, and things start looking pretty chaotic.
My personal view is that deterministic chaos is neat in toy problems (and a fun challenge for applying the method of manufactured solutions), but in the real world our uncertainties about everything (and the stochastic nature of many of the forcings) swamp the infinitesimals. The thing that makes the dynamics of the climate-policy-science “system” interesting is the tension between giving useful insight to decision makers and ensuring that insight is not overly sensitive to our inescapable uncertainties. Right now, the state of that system is far from equilibrium.
[Update: These survey results (courtesy of Roger Pielke Sr) are interesting. They seem to indicate that "climate scientists" view climate prediction as an IVP.The question is, 16. How would you rate the ability of global climate models to: (very poor 1 2 3 4 5 6 very good) 16c. model temperature values for the next 10 years 16d. model temperature values for the next 50 years. The mean response for the longer term prediction is actually lower than for the short term prediction (3.7 vs. 4.2), though the difference isn't that big considering the standard deviation.
The comparing the "reproduce observations" questions (16a. and 16b.) with the "predict future values" (16c. and 16d.) goes to the validation question. Would you bet your life on your models predictions?]





This comment from that thread deserves a closer look:
ReplyDelete“However, to communicate to policymakers that the models provide skillful multi-decadal regional and global predictions grossly oversells their capability. We can both agree that we should work to minimize the human alteration of the chemical composition of the Earth’s atmosphere, but still disagree whether we can skillfully predict the climate consequences of such actions.” (Pielke Sr.)
This is distinct from and more subtle than the usual “chaos fallacy” which reads something like “We can’t predict next week’s weather, so how can we make global warming forecasts 100 years out?:” It’s a fallacy nonetheless. It leaps to the conclusion that the theoretical possibility of long term chaos due to some undiscovered mechanism in the present climate regime (for which there is as yet no particular evidence, or any specific proposal) definitely trumps the changes in decadal statistics arising from changes in the GHG increase.
That's not Pielke's point at all, his point is about skillfull regional predictions (exactly what he said, not some sort of new chaos fallacy). Why doesn't anyone in climate science listen when people worry about model validation for a particular purpose? The "man our model predicts global mean temperature real good" argument is like an aero engineer bragging about his Euler code predicting lift really well when the decision to invest in the project really depends on nailing the drag counts.
The initial part of this post was a little light on exactly why I think the weather is to climate as IVP is to BVP analogy is pedagogically unsound. The real distinction between the two is the functionals you are interested in, not the type of problem you are solving. If, in fact, climate predictions were about getting to the no-kidding solution of BVPs and time was only a convenient continuation parameter, then acceleration methods that give up time-accuracy would be appropriate. Things like local time-stepping, or doing away with the time derivative altogether and doing a Newton's method (of course then you'd probably introduce a pseudo-time because parameter continuation turns out to be pretty necessary to get robust convergence). I think it would be a little tough to argue that you would get physically meaningful statistics from a solution that wasn't at least approximately (even if only crudely) time-accurate.
ReplyDeleteJosh - interesting stuff. No time for a longer response right now, but I hope to be back in a couple of weeks, and will give it some thought then. Two quick ones though:
ReplyDelete"Why doesn't anyone in climate science listen when people worry about model validation for a particular purpose?"
They do, all the time - it's a central question in the modeling community. But you have to go and talk directly to the scientists to get this; there's so many people trying to distort their uncertainty that they've learned to be a bit more guarded in public. Which is a pity.
Have you seen the results of the ensemble project yet:
http://ensembles-eu.metoffice.com/docs/Ensembles_final_report_Nov09.pdf
Cheers,
Steve
Steve,
ReplyDeleteThanks for the link, I hadn't seen that yet.
But you have to go and talk directly to the scientists to get this; there's so many people trying to distort their uncertainty that they've learned to be a bit more guarded in public.
I've noticed that too; from what I've found, the primary literature is generally very reasonable. The spin tends to get out of control. That's why I like Pielke Jr's stance, "the best defense is to be accurate", there will always be useful-idiots and spin-meisters who will denigrate things they don't understand or sow confusion.
The other best defense is to disengage, which is ok for some people, they just don't like arguing / discussing, but you're right it's a pity more don't engage publicly (though if they were doing that they wouldn't be doing what they love, so it's not really just to expect them to). That's why the 'division of labor' question is another one the climate science / policy support community needs to come to terms with.
You're right Steve, the climate boys do care, it just doesn't get a lot of press.
ReplyDeleteAnother good bit from James' Empty Blog:
Lenny Smith gave a very entertaining rant on this topic, which I found very useful as I'd been aware of his scepticism for some time, but not quite understood the reasons for it. Just for clarity, he is not sceptical of the broad picture of global climate change in terms of the expected large-scale future warming, but rather of the ability of models to provide such detailed predictions as say "typical" weather time series for specific locations and seasons several decades ahead (which UKCIP is promising). As he further points out, the time scale on which credibility may be lost is not the decades it takes for such predictions to be falsified observationally, but rather the much shorter time scale over which someone produces a new, conflicting, prediction with the next "bigger and better" model. I've generally been thinking in terms of global and large regional scales, with variables such as (ok, exclusively) mean temperature so had not really considered the detailed predictability of local climate changes, but he certainly painted a very persuasive picture of the difficulty of this. Note this is not the trivial "weather versus climate" meme, but rather the question of whether a model can usefully inform on (eg) the longest sequence of consecutive hot days in a summer, when it simply does not adequately simulate the processes that control long sequences of hot days. It is the statistics of "weather" events such as these that actually matters to end-users, much more so than global annual mean surface temperature.
Smith is worried about "Validation for a particular purpose", just like Pielke Sr. (and me, if I may be so bold as to put myself in the same group as those two fellas).
In regards to the Lorenz system calculations, note that the time period during which the results can be considered to be an IVP is strongly dependent on the step size used for the calculations. I think calculations out to about 20 Lorenz Time Units ( LTU ) have been determined to be somewhat converged in some fuzzy sense with sufficiently small step size. If step sizes larger than that required to attain this level of convergence are used, the ensemble-averaging approach applied to the calculations would indicate that the boundary value problem range had been attained when in fact it has not. The BVP range is at about 20 LTU and beyond, by this criterion.
ReplyDeleteNote that critically important properties and characteristics of the response of chaotic ODEs ( some rough estimate of some kind of convergence ) are needed in order to estimate which response corresponds to an IVP range and which corresponds to BVP range. These properties and characteristics have only be determined for the extremely simple systems of ODEs for which chaotic response has been demonstrated. These demonstrations have not yet been conducted for temporal-spatial chaotic response of PDEs. I'll speculate that they will never be completed for GCMs.
When ensembles are constructed from output of several codes, using different models, ICs, step sizes, etc, how is it determined that the IVP and BVP ranges are coincident. Is it not possible that averaging of IVP with BVP ranges might occur?
Personally, I'm not comfortable whenever any aspects of any numerical solution method are functions of the step size. For these ill-posed IVPs, this seems to be a universal characteristic.
My interpretation is that the climate change community has simply adopted the chaotic-response paradigm by osmosis and have omitted the enormous amount of very difficult work necessary to show ( prove ) that it is the correct paradigm for the continuous systems of equations in the GCMs. While GCM output might kind-of look like chaotic response, so can the output from codes that 'solve' equations that cannot represent chaotic response. And, numbers generated with unstable numerical methods, numerical instabilities, exhibit exponential growth and that growth can be bounded by use of algebraic constructs in the coding.
Interesting and very difficult problems.
Dan,
ReplyDeleteYou bring up some good points. I didn't look at time-step convergence at all for this post. I just picked a step size that gave good looking results (since my scheme is L-stable, and I'm not asking anyone to spend money based on these results, I've got that 'artistic' freedom). Maybe I should do a post on the difficulty of converging a weather-like functional compared to a climate-like functional.
On IVP vs. BVP, you're killing me man! My whole point was that I don't think that distinction is useful or accurate. It is unfortunately common though, so I understand if you want to stick with it for convenient explication's sake.
When ensembles are constructed from output of several codes, using different models, ICs, step sizes, etc, how is it determined that the IVP and BVP ranges are coincident.
The next post that talks about that paper Steve linked. It discusses some results which showed that a random initialization was nearly as skillful as a 'realistic' initialization, but doing a good initialization still has a measurable improvement in skill even for 'climate' predictions. So even the 'big boys' are showing that the IVP vs. BVP distinction isn't really a good one.
Personally, I'm not comfortable whenever any aspects of any numerical solution method are functions of the step size.
That makes (at least) two of us.
My interpretation is that the climate change community has simply adopted the chaotic-response paradigm by osmosis and have omitted the enormous amount of very difficult work necessary to show ( prove ) that it is the correct paradigm
I'm not sure how much practical significance 'chaos' has, I think our realistic uncertainties are too large for it to matter (I'd be quite open to correction on this though).
While GCM output might kind-of look like chaotic response, so can the output from codes that 'solve' equations that cannot represent chaotic response.
I think you are on to something with this line of reasoning (you touch on it in some of your posts), chaotic 'looking' response can be a symptom of poorly resolved, but important physics.
numbers generated with unstable numerical methods, numerical instabilities, exhibit exponential growth and that growth can be bounded by use of algebraic constructs in the coding.
This is true, but I think the numerical stuff is worked out. Boyd's spectral methods book has an entertaining account of how some of it was (re)discovered in the early climate modeling work (I say rediscovered because this was something von Neumann figured out, echos of the Wegman report yet again, why don't those guys read anyone else's papers?). The upshot is that the truncation error can sometimes look like a backwards heat equation, and this will eventually 'blow-up' (you get NaNs and Infs in your solution). This has nothing to do with the physics and is totally an artifact of the numerical method (hence the still uncollected prize).
There's a lot of discussion about grid convergence in models in the background reports and papers for (e.g.) the Community Climate System Model, http://www.ccsm.ucar.edu/models/
ReplyDeleteThere has been a lot of work done on the Earth models, much of it specialized to various subsystems (ocean, land, atmosphere, interactions), and a fair bit on algorithms (extended Kalman work, for instance, and http://www.nar.ucar.edu/2008/ESSL/catalog/cgd/amp.php). There's an overview available at: http://www.linuxclustersinstitute.org/conferences/archive/2009/PDF/Dennis_88341.pdf
I don't think whether a Navier Stokes prize has been won or not is any statement on the state of progress. You don't need to solve things at N-S resolution to simulate globally, these wouldn't necessarily generalize to non-linear dynamics (ice shelf collapse), and there are lots of reasons why prizes are forgone. For instance, there are other more pertinent competitions: http://www-pcmdi.llnl.gov/uhrccs/
In short, solving the world or a set of ocean currents is a different problem than solving a river, and methods need to be adapted accordingly, including their figures of merit.
ekzept,
ReplyDeleteThanks for the links; the point about the unclaimed prize was about 'blow-up' not resolution, I probably could have been clearer.
You said:
solving the world or a set of ocean currents is a different problem than solving a river, and methods need to be adapted accordingly, including their figures of merit.
The sub-grid scale models and other parametarizations may be different, but this is just hand-waving. If you are solving a PDE, then verifying a calculation (of a verified code) with grid convergence is the sine qua non.
The unfortunate problem with climate models is that they don't actually do this. To re-emphasize Dan's point about uneasiness when the stuff you care about is still a function of the grid (from the CCSM FAQ):
The CCSM3.0 release officially supports three resolutions referred to as "T85_gx1v3", "T42_gx1v3", and "T31_gx3v5". For each resolution, multi-century control runs using all active models (a "B configuration") have been scientifically validated.
In other words, we tuned the model at each of three resolutions to give decent hindcasts. That's not exactly consistent with the encouraged state of the practice.
At least they are working on it:
Project: Simulation quality as a function of horizontal and vertical resolution
Another major evaluation focus in AMP is on simulation quality as a function of horizontal and vertical resolution. Jim Hack, Julie Caron, and John Truesdale have been examining the quality of the mean climate and its variability characteristics using the spectral dynamical core for horizontal resolutions ranging from T31 through T341. This work has demonstrated clear improvements in the simulated mean dynamical circulation when more a more traditional climate resolution of T42 is doubled to T85 (Hack et al., 2006). Variability metrics, however, are generally unchanged at the higher resolution. Furthermore, continued increases in horizontal resolution exhibit weaker responses in terms of simulation improvement, particularly with regard to the most serious systematic simulation errors. This appears to point to deficiencies in the treatment of parameterized physics as the principal source of these systematic errors. The resolution studies have demonstrated significant differences in the interaction of the dynamical core and the parameterized physics package as a function of horizontal resolution. To better explore these issues, Truesdale has incorporated modifications to the CAM so that a single-column model version of the CAM (known as SCAM) can be more seamlessly exploited. Recent work by Truesdale includes an analysis of hurricanes in the high-resolution (T341) CAM runs compared to statistics generated by the Nested Regional Climate Model (NRCM) runs. Studies using the CAM and SCAM at multiple resolutions are ongoing.
I'd still appreciate any links to the lit of any grid convergence type studies (I'm not trying to get you to do a lit review for me I promise, I'm just curious, and I've looked, using scholar.google.com, with no luck, maybe the climate science folks call it something else?).
At least one person has recently presented some 'motivational' work on verification to the folks at UCAR:
ReplyDeleteVerification through Adaptivity
Brian Carnes
Sandia National Laboratories
Joint work with Bart van Bloemen Waanders and Kevin Copps, Sandia National Laboratories
Verification of computational codes and calculations has become a major issue in establishing credibility of computational science and engineering tools. Adaptive meshes and time steps have become powerful tools for controlling numerical error and providing solution verification. This talk makes the case for using adaptivity to drive verification. Connections between numerical error and overall uncertainty are emphasized.
In the first part of the talk, an overview of verification using uniform grid studies is presented, including grid convergence and manufactured solutions. Then basic ideas of numerical error estimation and adaptivity are outlined, including goal-oriented approaches using the adjoint problem. Finally, examples are shown to illustrate the use of adaptivity to control numerical error in thermal, fluid, and solid mechanics applications.
Here's some slides the same guys presented at a different conference (roughly the same subject though).
To re-emphasize Dan's point (again) about uneasiness when the stuff you care about is still a function of the grid (emphasis added):
ReplyDeleteThe other approach [to adaptive mesh refinement] is motivated from the mathematical side. Assuming that a well defined partial differential equation is given, adaptive refinement of the approximation order or mesh width intends to equilibrate the numerical error. This approach requires that a consistent formulation of the error is available and also that a capable estimation of that error is feasible. It also requires that the numerical method together with the discretization of the problem are both convergent. This might not be the case in real life meteorological applications, where discrete models of sub-grid processes can destroy convergence.
-- Adaptive Atmospheric Modeling: Key Techniques in Grid Generation, Data Structures, and Numerical Operations with Applications
This sort of thing should make you very uneasy about unvalidated claims of predictive capability. This is an open research problem that is being worked though. For instance, Dr Curry has an interesting paper about water droplet terminal velocity parameterization [pdf], in which one of the stated goals is to get a continuous model to improve on older 'look-up table'-style discontinuous ones.
Here's the reason why I haven't been able to find grid convergence results for climate models, the past results have not been very 'encouraging' (emphasis added):
ReplyDeleteTo place any confidence in numerical simulations of climate, the horizontal and vertical resolution must be fine enough to accurately represent the phenomenological scales of motion of most importance to the climate system. A common spectral truncation used in global climate models is a 42-wave triangular truncation (T42), which can very accurately treat features and their horizontal derivatives down to approximately 950 km. Motion scales below this truncation limit must be treated in some other way, and generally enter the solution in the form of a forcing term. In a spectral model these “subgrid-scale” terms are evaluated on a transform grid whose grid intervals are directly related to the spectral truncation. In a T42 model the transform grid interval is approximately 300 km at the equator. These terms are almost always evaluated using parameterization techniques, which can be highly nonlinear and are generally functions of the explicitly resolved atmospheric state variables. Ideally, one would select a horizontal resolution for which the solutions are in a convergent regime; i.e., where additional increases in resolution would not greatly alter the solutions. Under such circumstances it might also be expected that the behavior of parameterized forcing terms would not significantly change with additional increases in resolution.
Exploration of global atmospheric simulation sensitivity to horizontal resolution goes back more than 30 years (Manabe et al. 1970), and has continued sporadically in the intervening years (e.g., Manabe et al. 1979; Boer and Lazare 1988; Boville 1991; Kiehl and Williamson 1991; Chen and Tribbia 1993). Most investigations have identified some systematic improvements related to increases in horizontal resolution. In an earlier version of the CAM, Williamson et al. (1995) showed that many statistics used to characterize 3 climate properties began to converge in the range of a T63 spectral truncation for midlatitudes. They also showed that scales of motion included at T63 and higher resolutions were needed to capture the nonlinear processes which drive some larger scale circulations. The more discouraging outcome of that investigation was that they were unable to demonstrate convergence for many other quantities, even at a T106 truncation.
So what do you do when you can't get grid convergence on the functionals you care about? You punt (twiddle your fudge factors):
One of the unique design goals for the CAM3 was to provide simulations with comparable large-scale fidelity over a range of horizontal resolutions. This is accomplished through modifications to adjustable coefficients in the parameterized physics package associated with clouds and precipitation.
CCSM CAM3 Climate Simulation Sensitivity to Changes in Horizontal Resolution
This paper, Numerically Converged Solutions of the Global Primitive Equations for Testing the Dynamical Core of Atmospheric GCMs, provides a test case demonstrating numerical convergence of a pseudo-spectral discretization for the governing equations commonly used in climate models (which are significantly simplified from the full-up hyperbolic conservation laws). The demonstrated convergence rate is only ~0.9, so there's likely still an ordered error, a discontinuity (but they add artificial viscosity so this is unlikely), or they aren't in the asymptotic range yet (this seems unlikely as well based on eye-balling their contour plots). They mention in the paper that mathematics rather than physics should be the focus of a verification test like this, but then they go on to worry about the 'realism' of the test. Use the method of manufactured solutions and stop worrying!
ReplyDeleteThis is worrisome:
To demonstrate that the converged numerical solution discussed above is not an artifact of the pseudospectral model that was used to compute it, we have adopted the practical expedient of computing a new set of numerical solutions to the identical set of equations and initial conditions but with a different numerical scheme.
Pielke Sr. has another good article on his site about validation and credibility. It mentions Lindzen's lament, and the problem of science-based decision making which relies on models unconstrained by reality. Also mentions that the IVP vs BVP analogy for the difference between climate and weather is starting to be recognized as incorrect.
ReplyDeleteA ways up thread I wrote:If you are solving a PDE, then verifying a calculation (of a verified code) with grid convergence is the sine qua non.
ReplyDeleteHere is Boyd's take on the matter:
Definition 16 (IDIOT) Anyone who publishes a calculation without checking it against an identical computation with smaller N OR without evaluating the residuals of the pseudospectral approximation via finite differences is an IDIOT.
Roger Pielke Sr has put up a short bit on the IVP/BVP distinction (he's also published on the subject, one paper titled 'climate prediction as an initial value problem' from way back in 1998), here's what he says:
ReplyDeleteThere is a fundamental difference in how scientists who have prompted the 2007 IPCC WG1 report view climate modeling and how other climate scientists view this modeling. The IPCC perspective is that numerical weather prediction is an initial value problem while climate prediction is a boundary value problem in which levels of atmospheric CO2 and aerosols are the primary “boundary forcing”. With this perspective, they claim that changes in the statistics of weather (and other climate features) can be skillfully predicted.
However, our research has shown this is a seriously flawed view as climate prediction is really an initial value problem.
It's neat to see his appropriately titled paper from '98, match up with the dawning realization from the big iron boys that, yes in fact the governing equations (the physics) tell you what type of problem you are solving, rather than your computational capabilities.
More by Pielke Sr on the IVP/BVP distinction in climate forecasting.
ReplyDeleteHello Josh .
ReplyDeleteI came to appreciate your open mind and your pragmatic approach to very complex problems .
That's why I am about to start a rather long post about a couple of fundamental things .
I will mostly tackle 2 issues :
- the chaos
- the IVP vs BVP point of view
I will try to stay at a very general level avoiding technicalities . It is much more important to get the general view right and I think that only very few climate model builders get the general view right . That of course dramatically lowers the probability to study relevant technicalities .
As I write on the fly , it will probably not be well structured so I apologize in advance .
1) The chaos
Unfortunately it is probably a fair statement to say that 90% or so of climate model builders don't know what they are talking about . This has for consequence that they draw wrong conclusion from right observation or the other way round . Especially notions of attractors , basins of attraction , stability , invariance are almost always misunderstood . Yet these are fundamental concepts. What is the chaos theory ?
Mathematically it is a study of a system of non linear ODE . Physically it is a study of system with non linear dynamics . This study uses the frame of a FINITE phase space where the state of the system describes an orbit function of time . The number of dimensions may be low (f.ex Lorenz or planetary orbits) or very high (statistical thermodynamics) but is always finite . A chaotic system is always out of equilibrium and no point on its orbit in the phase space is “nearer” or “farther” from some hypothetical equilibrium condition . On the contrary , systems at or near equilibrium can never be chaotic .
I will insist upon it and say it a second time : the variables are independent dimensions of the phase space function of time ONLY . The chaos will always appear in a system where at least one of the Lyapounov coefficients is positive . This is a necessary and sufficient condition . The result of chaos is that the trajectory of the system runs through a necessarily bounded region of the phase space along a trajectory that is impossible to be predicted deterministically . The subspace of the phase space where the orbits live is called an attractor . Generally an attractor is invariant , e.g its topology is independent from the initial conditions but it is of course dependent from the parameters/coefficients of the ODE . It may or may not be fractal but I won’t discuss this technicality farther .
As the time evolution of a chaotic system cannot be predicted deterministically and it is an impossibility of principle , the only way to progress is a stochastical description . Therefore the very fundamental tool to progress in the chaos theory is the ergodic theory . One cannot insist enough on the fact that the ergodicity is the single most important property of a chaotic system . Indeed ergodicity gives us the insurance of existence of an invariant PDF function in the phase space which gives us the probability of the system to find itself in a small volume around a point . Invariant means that this PDF neither depends on the initial conditions nor on time . As there is nothing that warrants us ergodicity , it is a miracle that so many dynamical systems have this property . The major example of non ergodicity are Hamiltonian dynamics (gravitational interaction in the N body problem) and in this case no statistical description is possible . From this observation follows that ergodicity can NEVER be assumed but must be demonstrated . However once it is demonstrated a consistent , robust statistical description is possible (thermodynamics works quite nicely , right ?) .
2) Schaos
ReplyDeleteNo , this is not a typo . I have chosen to use a different word Schaos to distinguish it from chaos that I have described above in 1) . The S goes for space because we have now extended the dynamics to the spatial domain . And unfortunately almost nothing of the chaos theory survived this extension to the spatial domain . Worst of all is that we lost the frame of the theory – the phase space - because it now became uncountably infinite dimensional (this just comes from the trivial observation that a PDE is equivalent to an uncountable infinity of ODEs) .
And with the phase space we lost everything that comes along – attractors , orbits , stability , invariance , ergodicity and what not . The only thing that survived is the sensibility to initial conditions which makes Schaos as deterministically unpredictable as chaos . But even that can no more be quantitatively and qualitatively explained by well defined concepts like the Lyapounov coefficients because we have no orbits in the phase space anymore . That’s why every time I hear or read the words “Lorenz and chaos” and “climate” used together , I can be sure that the person doesn’t know what he is talking about . The only point that Lorenz and climate have in common is that Lorenz was a meteorologist .
Schaos theory doesn’t exist . What comes nearest is fluid dynamics and LDS (lattice dynamical systems) . The latter tries to artificially create an equivalent of a phase space by considering that the system is described by N chaotic (chaos as defined in 1) oscillators situated on a spatial lattice and interacting with each other . It is very complex , and the few results are far from a Schaos theory . Such systems are generally not ergodic , if one agrees what an extension of ergodicity to S domain means … Clearly there are no invariant spatial structures which could play a role equivalent to the attractors in the chaos theory (just look at cigarette smoke) . It is not clear at all what a stochastic interpretation of Schaos should be .
Etc . So weather and climate are very probably schaotic but certainly not chaotic .
3) IVP , BVP and climate .
ReplyDeleteFirst I consider that distinguishing IVP and BVP is irrelevant . This distinction is just a technicality which may but must not impact existence and unicity of solutions to PDE or ODE . Actually from a physical point of view everything is IVP because when you observe a system , you have the state you observed at some t0 and the laws of nature who say how it evolves from there . BVP is a sophistication when you want that the system observes some kind of constraints . In any case a BVP is just an IVP to which we added an equation describing a constraint if this constraint (like f.ex no slip condition) is not already included implicitly in the laws of nature .
So weather is of course an IVP if one wants to use this terminology . But what is the climate ?
I will finish my post with this question because I admit that after 10 years of reading papers and books about climate , I still do not know what it is from the physical point of view . Well as I showed above , climate is clearly not chaos .
Climate might be Schaos but Schaos theory doesn’t exist . So what is left ?
Climate may be a time and space average of weather what one often reads . But then one must ask an obvious question . Is there something in the climate that is not already in weather ? If the answer is that there are slow phenomenons that are neglected in weather (because it won’t go beyond 2 or 3 days) but are taken in account in climate , then there is no qualitative difference between weather and climate . It is just a matter of constant coefficients that one allows to vary or additional equations . Then climate is weather with variable coefficients . This doesn’t make the former more predictable than the latter . Besides this definition NEVER answers how and why the temporal and spatial averaging intervals should be chosen and why a set of some particular averages should be more relevant than another .
Last , also often given definition is of the kind “Climate is an envelope of weather and constrains its variations” .
This definition is often given with analogies to Lorenzian chaos and attractors which , as we have already seen is horribly wrong .
From this definition follow other misconceptions , probably also guided by misunderstanding of Schaos , namely that the climate would be “stable” or that the system would tend to some kind of “equilibrium” .
Well both weather and climate are fundamentally out of equilibrium which is a condition of chaos as we have seen . As for “stability” it is ill defined – if stability means “stays in some interval” then it is trivial – chaotic systems also always “stay in some interval” . If it means invariant , then it is obviously wrong .
What stays is that what I see , is that “climatology” is just a numerical simulation of a fluid mechanics system on a grid on which one imposed the conservation of mass , energy and momentum . Then clearly every run will show states that look like climate or weather . The constructal theory with infinitely simpler model easily reproduces all major features of the general circulation too . It is trivial to simulate a system by observing conservation laws and perhaps a bit of subgrid parametrisations . Problem is precisely that it can NOT show something pathological even if what it shows might have in reality a probability of 0 . There where it becomes pathological is that there is no reason that a frequency for a particular state obtained in 1000 simulations corresponds to a probability that the real system realizes this particular state . There is actually no reason that there even exists an invariant PDF for states on some arbitrary grid (see what I wrote about ergodicity) . Because of that , the results of numerical simulations can’t be validated or invalidated by experience . This really doesn’t look very interesting to me .
Tom, you cover a lot of ground here. It'll probably take me a while to digest and respond; just wanted to let you know I appreciate your comments.
ReplyDeleteGmcrews
ReplyDeleteSorry but I can't speculate about that . I think that it can have something in common with the fact that the nature is often isotropic and homogeneous . It strikes me in the Kolmogorov turbulence theory . But really I have either too many or no clues . Both cases are not good .
Schaos is a word that I have made up for the purpose of this post . So actually there are only those people having read this post who know it :)
You must continue googling LDS . Try also coupled map lattices . Try Afraimovich and Bunimovich . There is not much because it is very hard and few people work on it . "Schaos theory" doesn't exist yet . So with these exceptions there is really nothing that permits to get a grip on "Schaos" .
Yes Hamiltonian systems are not dissipative .
This doesn't prevent them to be chaotic (e.g exponential divergence of trajectories) . The N body system is chaotic . The solar system is chaotic . However it is a special kind of chaos , a non ergodic chaos . There are also very important and interesting theorems (look up KAM theorem) .
I did not understand you last phrase . Or at least how it links to my post above .
Complexity is a thing unto itself . I would rather say the opposite - fluid dynamics is precisely the domain where it shows most . There is a reason why the Navier Stokes equations still resist even the most basic demonstration - namely existence of a smooth unique solution in the 3D case .
The N body system is not bad either - how complexity appears from only 3 points interacting by simple gravity (and the system is not ergodic) .
Adendum :
ReplyDeleteI almost forgot the most important . Yes a study of Hamiltonian systems is one of the most important things . It is a basis of about everything in physics - mechanics , statistical thermodynamics , quantum mechanics and it plays a role even in the chaos theory (not "Schaos") .
Not knowing well Hamiltonian systems in physics is equivalent to not knowing well the alphabet in reading .
Survey results indicate climate scientists see climate prediction more as an IVP than a BVP.
ReplyDeleteInteresting comment that touches on the behavior of functionals of chaotic system state.
ReplyDeleteI may have been looking for something that doesn't exist:
ReplyDeleteClimate models are not verified or validated but updated and modified as new information becomes available.
Constructing Climate Knowledge with Computer Models
Model imperfections, coupled with fundamental limitations on the initial-value prediction of chaotic weather and the unknown path that society may take in terms of future emissions of greenhouse gases, imply that it is not possible to be certain about future climate.
ReplyDelete[...]
Ensembles, in which different initial conditions are sampled (recognizing the sensitive dependence on initial conditions in atmospheric flows), are now routinely produced and used in risk-based assessment of weather impacts. More recently, model uncertainties are also sampled. Hence, the extension to the climate problem is a natural one. Nevertheless, the key distinction is that for the weather forecasting problem, the ensemble prediction system may be verified over many cycles and may be corrected and improved. For the climate change prediction, no such verification is possible— a problem that has caused much debate about the best way to make predictions.
[...]
Climate models, at their heart, solve equations derived from physical laws, for example, the nonlinear Navier–Stokes equations of fluid flow. This is in contrast with some predictive models that may be purely based on the fitting of (perhaps complex) functions to data. Empirical approaches are not valid for climate change prediction as such models could not be reliably used to make extrapolations outside the historical training period (some authors even level this criticism at physically based models). Owing to finite computing capacity, approximations must be made to the equations and because they must be solved using computational techniques, certain processes must be simplified or parameterized for reasons of practicality (and here an element of empiricism can creep in).
Ensembles and probabilities: a new era in the prediction of climate change
Such understatement, the holistic tuning of all of the kludged together empricisims and sub-grid parameterizations is the only thing that makes the model give reasonable looking climates. It's not unreasonable to be skeptical of the predictive capabilities of such a mess.
Climate models, at their heart, solve equations derived from physical laws, for example, the nonlinear Navier–Stokes equations of fluid flow.
ReplyDeleteNo they don't . It is flabbergasting how somebody can make such an obviously wrong statement .
They cannot do that because the resolution (100 km) simply doesn't allow to solve any equation at all if it is not rigorously linear .
Such statements are just a propaganda with the intent to convey to ignorant people the idea that the models cannot be wrong beacuse what they do are rigorous mathematics (e.g "equation solving") and no sane person would dare to challenge a mathematical truth .
In fact this kind of statements generally means that "the dynamical core of climate models is inspired by results/insights obtained by studies of Navier-Stokes" .
For example in a 2D flow model one could be tempted to include in some discretized form the vorticity conservation even at with a grid of 100 km where the vorticity is a grossly estimated approximation .
But it should be obvious for everybody that these things have absolutely nothing in common with actually solving the equations !
Not that we know that there are unique regular solutions of Navier Stokes anyway (tongue in the cheek :))
Tom said: Such statements are just a propaganda with the intent to convey to ignorant people the idea that the models cannot be wrong beacuse what they do are rigorous mathematics (e.g "equation solving") and no sane person would dare to challenge a mathematical truth .
ReplyDeleteIn fact it's pretty good propaganda, because, coming from CFD, I assumed that they were actually solving NS until I actually took a look at the documentation for NCAR's community model and searched in vain for grid convergence studies. There are significant analytical simplifications that happen before discretization, and, as you point out, no one bothers finding a grid converged solution to the chosen equation set anyway.
I was looking up this oldie, but goodie for a young practitioner and found this interesting tidbit about grid convergence in the presence of sub-grid parameterizations:
ReplyDeleteFor these reasons, gridding guidelines will be based on physical and nu- merical arguments, rather than on demonstrations of convergence to a _right" answer. Grid convergence in LES is more subtle, or confusing, than grid convergence in DNS or RANS because in LES the variables are filtered quanti- ties, and therefore the Partial Differential Equation itself depends on the grid spacing. The order of accuracy depends on the quantity (order of derivative, inclusion of sub-grid-scale contribution), even without walls, and the situa- tion with walls is murky except of course in the DNS limit. We do aim at grid convergence for Reynolds-averaged quantities and spectra, but the sensitivity to initial conditions is much too strong to expect grid convergence of instantaneous fields (except for short times with closely defined initial conditions). In DES, we are not in a position to predict an order of accuracy when walls are involved; we cannot even produce the filtered equation that is being approximated. We can only offer the obvious statement that the full flow field is filtered, with a length scale proportional to A, which is the DES measure of grid spacing". This probably applies to any LES with wall modeling. Nevertheless, grid refinement is an essential tool to explore the soundness of this or any numerical approach.
Young Person's Guide to Detached-Eddy Simulation Grids
Way up in the third comment I said: I think it would be a little tough to argue that you would get physically meaningful statistics from a solution that wasn't at least approximately (even if only crudely) time-accurate.
ReplyDeleteLeonard Smith agrees: Given the nonlinearities involved, it is not clear whether a model that cannot produce reasonable “weather” can produce reasonable climate statistics of the kind needed for policy making, much less whether it can mimic climate change realistically.