Suppose you need to us an empirical closure for, say, the viscosity of your fluid or the equation of state. Usually you develop this sort of thing with some physical insight based on kinetic theory and lab tests of various types to get fits over a useful range of temperatures and pressures, then you use this relation in your code (generally without modification based on the code’s output). An alternative way to approach this closure problem would be to run your code with variations in viscosity models and parameter values and pick the set that gave you outputs that were in good agreement with high-entropy functionals (like an average solution state, there’s many ways to get the same answer, and nothing to choose between them) for a particular set of flows, this would be a sort of inverse modeling approach. Either way gives you an answer that can demonstrate consistency with your data, but there’s probably a big difference in the predictive capability between the models so developed.that is a surprisingly accurate description of the process actually used to tune parameters in climate general circulation models (GCMs).
Here's a relevant section from an overview paper [pdf]:
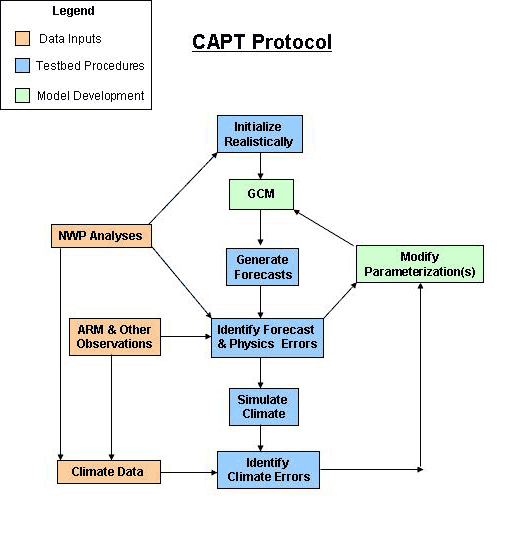
The CAPT premise is that, as long as the dynami- cal state of the forecast remains close to that of the verifying analyses, the systematic forecast errors are predominantly due to deficiencies in the model parameterizations. [...] In themselves, these differences do not automatically determine a needed parameterization change, but they can provide developers with insights as to how this might be done. Then if changing the parameterization is able to render a closer match between parameterized variables and the evaluation data, and if this change also reduces the systematic forecast errors or any compensating errors that are exposed, the modified parameterization can be regarded as more physically realistic than its predecessor.The highlighted conclusion is the troublesome leap. The process is an essentially post-hoc procedure based on goodness of fit rather than physical insight. This is contrary to established best practice in developing simulations with credible predictive capability. Sound physics rather than extensive empirical tuning is paramount if we're to have confidence in predictions. The paper also provides some discussion that goes to the IVP/BVP distinction:
But will the CAPT methodology enhance the performance of the GCM in climate simulations? In principle, yes: modified parameterizations that reduce systematic forecast errors should also improve the simulation of climate statistics, which are just aggregations of the detailed evolution of the model [see my comment here]. [...] Some systematic climate errors develop more slowly, however. [...] It follows that slow climate errors such as these are not as readily amenable to examination by a forecast-based approach.Closing the loop on long-term predictions is tough (this point is often made in the literature, but rarely mentioned in the press). The paper continues:
Thus, once parameterization improvements are provisionally indicated by better short-range forecasts, enhancements in model performance also must be demonstrated in progressively longer (extended-range, seasonal, interannual, decadal, etc.) simulations. GCM parameterizations that are improved at short time scales also may require some further "tuning" of free parameters in order to achieve radiative balance in climate mode.The discussion of data assimilation, initialization and transfer between different grid resolutions that follows that section is interesting and worth a read. They do address one of the concerns I brought up in my discussion with Robert, which was model comparison based on high-configurational-entropy functionals (like a globally averaged state):
If a modified parameterization is able to reduce systematic forecast errors (defined relative to high-duality observations and NWP analyses), it then can be regarded as more physically realistic than its predecessor.Please don't misunderstand my criticism, the process described is a useful part of the model diagnostic toolbox. However, it can easily fool us into overconfidence in the simulation's predictive capability, because we may mistake what is essentially an extensive and continuous model calibration process for validation.
Josh,
ReplyDeleteI added a comment to this thread:
http://www.easterbrook.ca/steve/?p=1388
To be fair, they (in the CAPT process for example) are actually looking at more than just a globally averaged state, they are looking at spatial and temporal error patterns too, but I think the basic criticism still applies.
ReplyDeleteHere's an interesting paper, Parameter Estimation for Differential Equations: A Generalized Smoothing Approach
ReplyDeleteSummary. We propose a new method for estimating parameters in non-linear differential equations. These models represent change in a system by linking the behavior of a derivative of a process to the behavior of the process itself. Current methods for estimating parameters in differential equations from noisy data are computationally intensive and often poorly suited to statistical techniques such as inference and interval estimation. This paper describes a new method that uses noisy data to estimate the parameters defining a system of nonlinear differ- ential equations. The approach is based on a modification of data smoothing methods along with a generalization of profiled estimation. We derive interval estimates and show that these have good coverage properties on data simulated from chemical engineering and neurobiology. The method is demonstrated using real-world data from chemistry and from the progress of the auto-immune disease lupus.
Keywords: Differential equations, profiled estimation, estimating equations, Gauss-Newton methods, functional data analysis
The focus is on ODEs, but many of the considerations carry-over to PDEs:
The insolvability of most ODE’s has meant that statistical science has had little impact on the fitting of such models to data. Current methods for estimating ODE’s from noisy data are often slow, uncertain to provide satisfactory results, and do not lend themselves well collateral analyses such as interval estimation and inference. Moreover, when only a subset of variables in a system are actually measured, the remainder are effectively functional latent variables, a feature that adds further challenges to data analysis. Finally, although one would hope that the total number of measured values, along with its distribution over measured values, would have a healthy ratio to the dimension of the parameter vector θ, such is often not the case. Measurements in biological, medical and physiology, for example, may require invasive or destructive procedures that can strictly control the number of measurements that can realistically be obtained. These problems can be often be offset, however, by a high level of measurement precision.
Dan makes a good point about the difference between parameters that are a property of the fluid and those that are a property of the flow.
ReplyDeleteHere's another that's focused on PDEs, PARAMETER IDENTIFICATION TECHNIQUES FOR PARTIAL DIFFERENTIAL EQUATIONS:Many physical systems exhibiting nonlinear spatiotemporal dynamics can be modeled by partial differential equations. Although information about the physical properties for many of these systems is available, normally not all dynamical parameters are known and, therefore, have to be estimated from experimental data. We analyze two prominent approaches to solve this problem and describe advantages and disadvantages of both methods. Specifically, we focus on the dependence of the quality of the parameter estimates with respect to noise and temporal and spatial resolution of the measurements. Keywords: Parameter estimation; partial differential equations; spatio-temporal systems; non- linear dynamics; complex Ginzburg–Landau equation.
A Comprehensive Validation Methodology for Sparse Experimental Data
ReplyDeleteAbstract:A comprehensive program of verification and validation has been undertaken to assess the applicability of models to space radiation shielding applications and to track progress as models are developed over time. The models are placed under configuration control, and automated validation tests are used so that comparisons can readily be made as models are improved. Though direct comparisons between theoretical results and experimental data are desired for validation purposes, such comparisons are not always possible due to lack of data. In this work, two uncertainty metrics are introduced that are suitable for validating theoretical models against sparse experimental databases. The nuclear physics models, NUCFRG2 and QMSFRG, are compared to an experimental database consisting of over 3600 experimental cross sections to demonstrate the applicability of the metrics. A cumulative uncertainty metric is applied to the question of overall model accuracy, while a metric based on the median uncertainty is used to analyze the models from the perspective of model development by analyzing subsets of the model parameter space.
On the intersection between V&V and sound software carpentry:
The degree of confidence in a model is not only an issue of accuracy, but also of the rigor and completeness of the assessment itself. An essential aspect of a comprehensive validation effort is the development of configuration-controlled verification and validation (V&V) test cases. Configuration control (also called configuration management) is a process in which consistency is established for a product (i.e. a model or a software suite), and any changes made to the product are tracked. The effects of the changes on the product are documented, and therefore, problems caused by changes to the product can be backtracked. The models reviewed in this paper have been placed under configuration control with the criteria that the V&V test cases will be run when significant changes are made to those models. This approach allows accuracy to be tracked across the relevant range of applications and avoid situations where model changes intended for a specific calculation or application actually decrease the overall accuracy. In addition, it will enable more complete accuracy assessments to measure progress against goals as the models and codes are updated and as new data become available for validation. It also helps ensure model results are repeatable.
Lucia has a good post explaining this calibration / validation distinction with her simple one parameter model of the climate.
ReplyDeleteI've spent some time ( >10 years) designing and building pattern classifiers. I see some similarities between my field and the climate-model field in that we often have an incomplete set of noisy data, we only generally know what the output should look like, and are not exactly sure how to get from one to the other. Both fields employ a lot of math, statistics, and intuition, to get the aproximation of a function that will get us from point A to point B.
ReplyDeleteIn many areas of classification research there are standard ground-truth data sets that help provide a common measure of how classifiers perform in 'the real world'.
If the climate model approximations were built using data up to 1980, and data from 1980 onward was reserved for validation purposes only, couldn't these various models be tested objectively for their accuracy? Or am I missing something specific to climate models?
Hi Will, thanks for your comment. You are right, climate modeling has similarities across lots of different fields (hence the ability of interested amateurs to understand the lit fairly easily).
ReplyDeleteThat article I linked at Lucia's right before your comment describes why 'hold out' data like what you suggest is never really independant (which is also something recognized in the climate modeling lit). That's why computational physics communities (with climate modelers as a notable exception) have settled on a best practice of skillful prediction as a measure of validation. Rather than a cross-validation sort of approach.
Thank you for the reply, and excellent links, jstults. Lucias decription is very well written and indeed sounds like a common recipe I've used many times myself.
ReplyDeleteI am still scratching my head over Riechler and Kims comment regarding the data. Specifically "Present climate, however, is not an independent data set since it has already been used for the model development(Willamson 1995)".
I can see how cross-validation might pose a problem, but I have to ask: Why not redo a model (or at least redo one of the models) without incorporating new data? I'm not familiar with computational phsyics, so please forgive my question if it sounds stupid. :)
There also seems to be some question as to what parameters/features need to be included in the parameterization models. I would be very interested to know if anyone has attempted a computational approach to feature selection. It would seem logical given that we seem to be wading into Bayes territory anyway. :)
Great Blog BTW. I'm adding it to my list of favorites!
Should be 'physics' not 'phsyics'. :)
ReplyDeleteI am still scratching my head over Riechler and Kims comment regarding the data. Specifically "Present climate, however, is not an independent data set since it has already been used for the model development(Willamson 1995)".
ReplyDeleteI can see how cross-validation might pose a problem, but I have to ask: Why not redo a model (or at least redo one of the models) without incorporating new data?
Often the data is not used explicitly in a parameter fitting exercise, but it can implicitly guide the choices of and simplifications to the governing equations (climate models are a couple simplifications removed from the fully general conservation laws, and there's lots of processes going on besides just air and water flow). So it's hard to tease out exactly what choices are influenced by knowledge of what data.
I think there's lots of promise in going towards Bayes methods because that tends to make the influence of the current state of knowledge on our choices more explicit.
I would be very interested to know if anyone has attempted a computational approach to feature selection.
I'd be interested to know that too; please share any links if you find them.
Glad you like the site; I've been a little slow lately in adding more toy problem results (real life intervenes every now and then on the blogging), but hope to get back to doing it more regularly.
Will,
ReplyDeleteI think you'd be interested in Model Selection: Beyond the Bayesian/Frequentist Divide. Section four addresses how cross-validation is really just adding another level to the inference (a hyper-parameter if you are Bayesian). There's still no general solution to the problem of predicting performance or generalization risk. Which is the technical way of saying "calibration is not validation."
George Crews was kind enough to link this post from a discussion on W.M. Briggs' site. This more recent post here touches on many of the same concepts.
ReplyDelete