A few of the sections from Chapter 21 of Jayne’s book are reproduced below. The topic is such an important one to the practicing engineer / scientist, yet orthodox robust regression is a nearly impenetrable mess of ad hoceries. In comparison, the treatment of outliers is quite straight-forward in a Bayesian framework.
21.3 The two-model model
We have a ’good’ sampling distribution
 | (21.2) |
with a parameter θ that we want to estimate. Data drawn urn-wise from G(x|θ) are called ’good’ data. But there is a ’bad’ sampling distribution
 | (21.3) |
possibly containing an uninteresting parameter η. Data from B(x|η) are called ’bad’ data; they appear to be useless or worse for estimating θ, since their probability of occurring has nothing to do with θ. Our data set consists of n observations
 | (21.4) |
But the trouble is that some of these data are good and some are bad, and we do not know which (however, we may be able to make guesses: an obvious outlier – far out in the tails of G(x|θ) – or any datum in a region of x where G(x|θ) ≪ B(x|η) comes under suspicion of being bad).
In various real problems we may, however, have some prior information about the process that determines whether a given datum will be good or bad. Various probability assignments for the good/bad selection process may express that information. For example, we may define
 | (21.5) |
and then assign joint prior probabilities
 | (21.6) |
to the 2n conceivable sequences of good and bad.
21.4 Exchangeable selection
Consider the most common case, where our information about the good/bad selection process can be represented by assigning an exchangeable prior. That is, the probability of any sequence of n good/bad observations depends only on the numbers r, (n - r) of good and bad ones, respectively, and not on the particular trials at which they occur. Then the distribution 21.6 is invariant under permutations of the qi, and by the de Finetti representation theorem (Chapter 18), it is determined by a single generating function
g(u):
 | (21.7) |
It is much like flipping a coin with unknown bias where, instead of ’good’ and ’bad’, we say ’heads’ and ’tails’. There is a parameter u such that if u were known we would say that any given datum x may, with probability u, have come from the good distribution; or with probability (1 - u) from the bad one. Thus, u measures the ’purity’ of our data; the closer to unity the better. But u is unknown, and g(u) may, for present purposes, be thought of as its prior probability density (as was, indeed, done already by Laplace; further technical details about this representation are given in Chapter 18). Thus, our sampling distribution may be written as a probability mixture of the good and bad distributions:
 | (21.8) |
This is just a particular form of the general parameter estimation model, in which θ is the parameter of interest, while (η,u) are nuisance parameters; it requires no new principles beyond those expounded in Chapter 6.
Indeed, the model 21.8 contains the usual binary hypothesis testing problem as a special case, where it is known initially that all the observations are coming from G, or they are all coming from
B, but we do not know which. That is, the prior density for u is concentrated on the points u = 0,
u = 1:
 | (21.9) |
where p0 = p(H0|I), p1 = 1 - p0 = p(H1|I) are the prior probabilities for the two hypotheses:
 | (21.10) |
Because of their internal parameters, they are composite hypotheses; the Bayesian analysis of this case was noted briefly in Chapter 4. Of course, the logic of what we are doing here does not depend on value judgements like ’good’ or ’bad’.
Now consider u unknown and the problem to be that of estimating θ. A full non-trivial Bayesian solution tends to become intricate, since Bayes’ theorem relentlessly seeks out and exposes every factor that has the slightest relevance to the question being asked. But often much of that detail contributes little to the final conclusions sought (which might be only the first few moments, or percentiles, of a posterior distribution). Then we are in a position to seek useful approximate algorithms that are ’good enough’ without losing essential information or wasting computation on non-essentials. Such rules might conceivably be ones that intuition had already suggested, but, because they are good mathematical approximations to the full optimal solution, they may also be far superior to any of the intuitive devices that were invented without taking any note of probability theory; it depends on how good that intuition was.
Our problem of outliers is a good example of these remarks. If the good sampling density
G(x|θ) is very small for |x| < 1, while the bad one B(x|η) has long tails extending to |x|≫ 1, then any datum y for which |y| > 1 comes under suspicion of coming from the bad distribution, and intuitively one feels that we ought to ’hedge our bets’ a little by giving it, in some sense, a little less credence in our estimate of θ. Put more specifically, if the validity of a datum is suspect, then intuition suggests that our conclusions ought to be less sensitive to its exact value. But then wee have just about stated the condition of robustness (only now, this reasoning gives it a rationale that was previously missing). As |x|→∞ it is practically certain to be bad, and intuition probably tells us that we ought to disregard it altogether.
Such intuitive judgments were long since noted by Tukey and others, leading to such devices as the ’re-descending psi function’, which achieve robust/resistant performance by modifying the data analysis algorithms in this way. These works typically either do not deign to note even the existence of Bayesian methods, or contain harsh criticism of Bayesian methods, expressing a belief that they are not robust / resistant and that the intuitive algorithms are correcting this defect – but never offering any factual evidence in support of this position.
In the following we break decades of precedent actually examining a Bayesian calculation of outlier effects, so that one can see – perhaps for the first time – what Bayesianity has to say about the issue, and thus give that missing factual evidence.
21.5 The general Bayesian solution
Firstly, we give the Bayesian solution based on the model 21.8 in full generality, then we study some special cases. Let f(θηu|I) be the joint prior density for the parameters. Their joint posterior density given the data D is
 | (21.11) |
where A is a normalizing constant, and, from 21.8,
![n ∏ L (θ, η, u) = [uG (xi|θ) + (1 - u)B (xi|η )] i=1](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjAhYInKyLSUHCQTrpZ5f7vt8s-N58z1oHIH2qq4280tMtyWeaXmEyeiWZv0OZ2HmmlJmgBhw20bYn8wZikQWRKtZqnq-9XQ8KpEJp1tcmyxSLb1PldsKM7LNw0wBEsQTervNUqipDwijo/s400/outlier10x.png) | (21.12) |
is their joint likelihood. The marginal posterior density for θ is
 | (21.13) |
To write 21.12 more explicitly, factor the prior density:
 | (21.14) |
where f(θ|I) is the prior density for θ, and h(η, u|θ, I) is the joint prior for (η,u), given θ. Then the marginal posterior density for θ, which contains all the information that the data and the prior information have to give us about θ, is
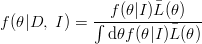 | (21.15) |
where we have introduced the quasi-likelihood
 | (21.16) |
Inserting 21.12 into 21.16 and expanding, we have
![[ ¯L(θ) = ∫∫ dηdu h (η, u |θ, I) unL(θ) + un- 1(1 - u) ∑n B (x |η)L (θ) n-2 2∑ j=1 j j +u (1 - u) j<k B (xj|η )B (xk|η)Ljk(θ) + ⋅⋅⋅ + (1 - u)nB (x1|η)⋅⋅⋅B (xn|η)]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOm2ZxCrJaCyZa8bPGV5FGtysLclYdWhIejzyTRuKa_zhjC85m6f8QTm_5ComsUDhMIGHmjYWxU7nh680_6z9Zr98UaNaZvDOP2pJCavIF3Dvf4TJ6QepGakwSTK-36jXsXnY-tO1A0NA/s400/outlier15x.png) | (21.17) |
in which
 | (21.18) |
are a sequence of likelihood functions for the good distribution in which we use all the data, all except the datum xj, all except xj and xk, and so on. To interpret the lengthy expression 21.17, note that the coefficient of L(θ),
 | (21.19) |
is the probability, conditional on θ and the prior information, that all the data {x1,…,xn} are good. This is represented in the Laplace-de Finetti form 21.7 in which the generating function g(u) is the prior density h(u|θ, I) for u, conditional on θ. Of course, in most real problems this would be independent of θ (which is presumably some parameter referring to an entirely different context than u); but preserving generality for the time being will help bring out some interesting points later.
Likewise, the coefficient of Lj(θ) in 21.17 is
 | (21.20) |
now the factor
 | (21.21) |
is the joint probability density, given I and θ, that any specified datum xj is bad, that the (n- 1) others are good, and that η lies in (η,η + dη). Therefore the coefficient 21.20 is the probability, given I and θ, that the jth datum would be bad and would have the value x
j, and the other data would be good. Continuing in this way, we see that, to put it in words, our quasi-likelihood is:
 | (21.22) |
In shorter words: the quasi-likelihood  (θ) is a weighted average of the likelihoods for the good distribution G(x|θ) resulting from every possible assumption about which data are good, and which are bad, weighted according to the prior probabilities of those assumptions. We see how every detail of our prior knowledge about how the data are being generated is captured in the Bayesian solution.
(θ) is a weighted average of the likelihoods for the good distribution G(x|θ) resulting from every possible assumption about which data are good, and which are bad, weighted according to the prior probabilities of those assumptions. We see how every detail of our prior knowledge about how the data are being generated is captured in the Bayesian solution.
This result has such wide scope that it would require a large volume to examine all its implications and useful special cases. But let us note how the simplest ones compare to our intuition.
21.6 Pure Outliers
Suppose the good distribution is concentrated in a finite interval
 | (21.23) |
while the bad distribution is positive in a wider interval which includes this. Then any datum x for which |x| > 1 is known with certainty to be an outlier, i.e. to be bad. If |x| < 1, we cannot tell with certainty whether it is good or bad. In this situation our intuition tells us quite forcefully: Any datum that is known to be bad is just not part of the data relevant to estimation of θ and we shouldn’t be considering it at all. So just throw it out and base our estimate on the remaining data.
According to Bayes’ theorem this is almost right. Suppose we find xj = 1.432, xk = 2.176, and all the other x’s less than unity. Then, scanning 21.24 it is seen that only one term will survive:
 | (21.24) |
As discussed above, the factor Cjk is almost always independant of θ, and since constant factors are irrelevant in a likelihood, our quasi-likelihood in 21.15 reduces to just the one obtained by throwing away the outliers, in agreement with that intuition.
But it is conceivable that in rare cases Cjk(θ) might, after all, depend on θ; and Bayes’ theorem tells us that such a circumstance would make a difference. Pondering this, we see that the result was to be expected if only we had thought more deeply. For if the probability of obtaining two outliers with values xj, xk depends on θ, then the fact that we got those particular outliers is in itself evidence relevant to inference about
θ.
Thus, even in this trivial case Bayes’ theorem tells us something that unaided intuition did not see: even when some data are known to be outliers, their values might still, in principle, be relevant to estimation of θ. This is an example of what we meant in saying that Bayes’ theorem relentlessly seeks out and exposes every factor that has any relevance at all to the question being asked.
In the more usual situations, Bayes’ theorem tells us that whenever any datum is known to be an outlier, then we should simply throw it out, if the probability of getting that particular outlier is independent of θ. For, quite generally, a datum xi can be known with certainty to be an outlier ony if G(xi|θ) = 0 for all θ; but in that case every likelihood in 21.24 that contains xi will be zero, and our posterior distribution for θ will be the same as if the datum xi had never been observed.
21.7 One receding datum
Now suppose the parameter of interest is a location parameter, and we have a sample of ten observations. But one datum xj moves away from the cluster of the others, eventually receding out 100 standard deviations of the good distribution G. How will our estimate of θ follow it? The answer depends on which model we specify.
Consider the usual model in which the sampling distribution is taken to be simply G(x|θ) with no mention of any other ’bad’ distribution. If G is Gaussian, x ≈ N(θ,σ), and our prior for θ is wide (say > 1000σ), then the Bayesian estimate for quadratic loss function will remain equal to the samaple average, and our far-out datum will pull the estimate about ten standard deviations away from the average indicated by the other nine data values. This is presumably the reason why Bayesian methods are sometimes charged with failure to be robust/resistant.
However, that is the result only for the assumed model, which in effect proclaims dogmatically: I know in advance that u = 1; all the data will come from G, and I am so certain of this that no evidence from the data could change my mind. If one actually had this much prior knowledge, then that far-out datum would be highly significant; to reject it as an ’outlier’ would be to ignore cogent evidence, perhaps the most cogent piece of evidence that the data provide. Indeed, it is a platitude that important scientific discoveries have resulted from an experiment having that much confidence in his apparatus, so that surprising new data were believed; and not merely rejected as ’accidental’ outliers.
If, nevertheless, our intuition tells us with overwhelming force that the deviant datum should be thrown out, then it must be that we do not really believe that u = 1 strongly enough to adhere to it in the face of the evidence of the surprising datum. A Bayesian may correct this by use of the more realistic model 21.8. Then the proper criticism of the first procedure is not of Bayesian methods, but rather of the saddling of Bayesian methodology with an inflexible, dogmatic model which denies the possibility of outliers. We saw in Section 4.4 on multiple hypothesis testing just how much difference it can make when we permit the robot to become skeptical about an overly simple model.
Bayesian methods have inherent in them all the desirable robust/resistant qualities, and they will exhibit these qualities automatically, whenever they are desirable – if a sufficiently flexible model permits them to do so. But neither Bayesian nor any other methods can give sensible results if we put absurd restrictions on them. There is a moral in this, extending to all of probability theory. In other areas of applied mathematics, failure to notice some feature (like the possibility of the bad distribution B) means only that it will not be taken into account. In probability theory, failure to notice some feature may be tantamount to making irrational assumptions about it.
Then why is it that Bayesian methods have been criticized more than orthodox ones on this issue? For the same reason that city B may appear in the statistics to have a higher crime rate than city A, when the fact is that city B has a lower crime rate, but more efficient means for detecting crime. Errors undetected are errors uncriticized.
Like any other problem in this field, this can be further generalized and extended endlessly, to a three-model model, putting parameters in 21.6, etc. But our model is already general enough to include both the problem of outliers and conventional hypothesis testing theory; and a great deal can be learned from a few of its simple special cases.




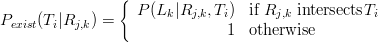










![n ∏ L (θ, η, u) = [uG (xi|θ) + (1 - u)B (xi|η )] i=1](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjAhYInKyLSUHCQTrpZ5f7vt8s-N58z1oHIH2qq4280tMtyWeaXmEyeiWZv0OZ2HmmlJmgBhw20bYn8wZikQWRKtZqnq-9XQ8KpEJp1tcmyxSLb1PldsKM7LNw0wBEsQTervNUqipDwijo/s400/outlier10x.png)


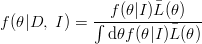

![[ ¯L(θ) = ∫∫ dηdu h (η, u |θ, I) unL(θ) + un- 1(1 - u) ∑n B (x |η)L (θ) n-2 2∑ j=1 j j +u (1 - u) j<k B (xj|η )B (xk|η)Ljk(θ) + ⋅⋅⋅ + (1 - u)nB (x1|η)⋅⋅⋅B (xn|η)]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOm2ZxCrJaCyZa8bPGV5FGtysLclYdWhIejzyTRuKa_zhjC85m6f8QTm_5ComsUDhMIGHmjYWxU7nh680_6z9Zr98UaNaZvDOP2pJCavIF3Dvf4TJ6QepGakwSTK-36jXsXnY-tO1A0NA/s400/outlier15x.png)





 (
(








