Treating Image Edges

There are some good examples floating around of creating customized image processing kernels in the python imaging library (PIL). It's very convenient to simply define your own mask, and the library takes care of the convolution.

One drawback is that the edges don't get filtered in this process. There are various ad-hoc things you can do. You can just drop a line of pixels all the way around the picture, so the gradient image of a 800x600 picture would be 798x598 pixels (if you're using a compact stencil), or you could just copy the edge pixels from the old picture to the new picture. So in effect, the edges don't get filtered. For most applications this is probably no big deal, but it might be, and we can do better.

All we have to do is change our difference operator for the edge pixels, use a forward or backward difference on the edges rather than the central differences used on the interior. Then you get gradient info for your edge pixels too!

Customizing the PIL kernel class has been done, so I'm going to use Fortran90 and F2Py for my difference operators. I'll still use the PIL for all of the convenient image reading/writing utilities though. No need to implement that in Fortran!

We can use our little Maxima script to generate the differences we need on the edges. If you've taken a basic numerical methods course you'll probably recognize them as the three point forward and backward difference approximations for the first derivative.



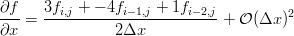
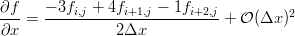
The Python to do just that is here:

import sys, math, Image, numpy
from filters import *


if __name__ == '__main__':
in_img = Image.open(sys.argv[1])
in_img = in_img.convert("L")
out_img = Image.new("L", in_img.size)
pix = in_img.getdata()
# put the pixels into a fortran contiguous array:
pix_array = numpy.array(pix)
pix_array = pix_array.reshape( in_img.size, order='F' )
# calculate the gradient
g = first_order_gradient(pix_array,in_img.size[0],in_img.size[1])
gmag = 255 - numpy.sqrt( g[0,:,:]*g[0,:,:] + g[1,:,:]*g[1,:,:] )
gmag.astype("int")
# pack the gradient magnitude into a new image
out_img.putdata( gmag.reshape( gmag.size, order='F' ) )
out_img.save(sys.argv[2])

Where I've used F2Py to generate the filters module from a Fortran90 file. The module defines the subroutine first_order_gradient(), which implements the ideas discussed above. The gradients on the interior points are calculated using a central difference:

! apply the central operator to the interior pixels
do j = 2, nj-1
do i = 2, ni-1
g(1,i,j) = (in_image(i+1,j) - in_image(i-1,j)) / 2.0
g(2,i,j) = (in_image(i,j+1) - in_image(i,j-1)) / 2.0
end do
end do

The gradients along the edges are calculated using the forward and backward differences (only x edges shown for brevity):

! loop over the y dimension and apply the asymmetric operators to the
! x min and x max edges
do j = 2, nj-1 ! leave out the corners
i = 1 ! minimum edge, go forward
g(1,i,j) = (-3.0*in_image(i,j) + 4.0*in_image(i+1,j) - in_image(i+2,j))/2.0
i = ni ! maximum edge, go backward
g(1,i,j) = (3.0*in_image(i,j) - 4.0*in_image(i-1,j) + in_image(i-2,j))/2.0
! no change for the y derivative
i = 1
g(2,i,j) = (in_image(i,j+1) - in_image(i,j-1)) / 2.0
i = ni
g(2,i,j) = (in_image(i,j+1) - in_image(i,j-1)) / 2.0
end do

Finally the four corners are calculated separately, because each one has a unique combination of stencils required. Putting the loops in Fortran speeds things up considerably compared to the pure Python implementations I did before. Here is the gradient magnitude of the dials from Poor Man's ADC calculated with the above technique:

Sobel, Scharr and Truncation Error

In image processing the discrete difference operators to calculate gradients and second derivatives are called "masks". They are often referred to as "stencils" in other applications of finite differences for solving PDEs, estimating sensitivities, etc.

Some of the kernels (a mask plus particular values) for calculating gradients are Sobel:

[ 1 2 1]
Gy = [ 0 0 0]
[-1 -2 -1]

[ 1 0 -1]
Gx = [ 2 0 -2]
[ 1 0 -1]

or Sharr:

[ 3 10 3]
Gy = [ 0 0 0]
[-3 -10 -3]

[ 3 0 -3]
Gx = [ 10 0 -10]
[ 3 0 -3]

or the simpler stencil we used in the previous posts, which only used neighbouring pixels in one direction to estimate the gradient. What if we want to design our own masks? A useful tool is the multidimensional Taylor series:

In two dimensions we have:

which includes up to third order terms. We can't actually include the two pure third order terms because we only have three points in either the x or y direction, and we need a minimum of four. We can include the mixed third order terms though, so that gives us 8 constraints on our coefficients. Instead of including all 9 points in the stencil we have to drop one, so in the Maxima code below you'll notice that the central point is commented out.

Lets examine the truncation error for the two masks above. First we define a vector of delta x and delta y corresponding to each point in the stencil:

/* define the points in the stencil or mask: */
steps : matrix( /* dx, dy */
[-1, 1],
[0, 1],
[1, 1],
[-1, 0],
/* [0,0], */
[1, 0],
[-1, -1],
[0,-1],
[1, -1] );

Then vectors describing the coefficients in the two masks (we'll just use the y-component for this example):

/* coefficients in sobel mask */
sobel_y : matrix(
[1],
[2],
[1],
[0],
/*[0],*/
[0],
[-1],
[-2],
[-1]
);
/* coefficients in sharr mask */
sharr_y : matrix(
[3],
[10],
[3],
[0],
/*[0],*/
[0],
[-3],
[-10],
[-3]
);

To evaluate the truncation error we also need to create an operator that is based on the multidimensional Taylor series shown above. This will let us simply multiply those vectors by the operator to see what the masks are actually estimating. Here's the operator:

n : matrix_size( steps );
A : zeromatrix(n[1],n[1]);

for j : 1 thru n[1] do ( A[1,j] : 1 );/* f */
for j : 1 thru n[1] do ( A[2,j] : steps[j,1] );/* df/dx */
for j : 1 thru n[1] do ( A[3,j] : steps[j,2] );/* df/dy */
for j : 1 thru n[1] do ( A[4,j] : steps[j,1]^2/2! );/* d2f/dx2 */
for j : 1 thru n[1] do ( A[5,j] : steps[j,2]^2/2! );/* d2f/dy2 */
for j : 1 thru n[1] do ( A[6,j] : 2*steps[j,1]*steps[j,2]/2! );/* d2f/dxdy */
for j : 1 thru n[1] do ( A[7,j] : 3*steps[j,1]*steps[j,2]^2/3! );/* d3f/dxdy2 */
for j : 1 thru n[1] do ( A[8,j] : 3*steps[j,1]^2*steps[j,2]/3! );/* d3f/dx2dy */

Now the truncation error terms are shown by a couple of matrix vector multiplies:

sobel_te : A.sobel_y;
sharr_te : A.sharr_y;

Rather than just getting a single non-zero entry in the third place of the resulting vector we get a non-zero entry in the last place as well. Looking back at our operator, this is the row for the third order mixed derivative term, (d^3 f)/(dx^2 dy). In other words both the Sobel and Sharr operators introduce an error in their estimation of the gradient that is proportional to this mixed derivative.

How to avoid this error? Well, we can choose a right hand side vector that only has a 1 in the third position and zeros everywhere else, and then invert our operator to solve for what the values in our mask should be.

/* define which derivative we want to estimate, constrain the unwanted
ones to be zero: */
derivs : matrix(
[0], /* f */
[0], /* df/dx */
[1], /* df/dy */
[0], /* d2f/dx2 */
[0], /* d2f/dy2 */
[0], /* d2f/dxdy */
[0], /* d3f/dx2dy */
[0] /* d3f/dxdy2 */
);
inv_A : invert(A);
coeffs : inv_A.derivs;

This gives a result with only non-zero coefficients for the points at [0,1] and [0,-1], in other words, the simple estimate we've already been using! There's really no need to include all those other points for the gradient calculation.

Open Source Tools

I just wanted to put in another plug for Maxima, the open source computer algebra system that I use regularly. The great thing about using an open source tool, other than customizability and the ability to "look under the hood", is the responsiveness of the user and developer community.

I found a little bug in the f90() function that caused it to use the old fixed-format FORTRAN77 style line continuation characters when outputting a long matrix expression (bug report) rather than the correct Fortran90 free-form style. I posted a bug report to the list on the 18th of October, I had a reply from another user who understood the problem that same day. A work-around was posted (here by me), and the fix was committed to the code on the 24th of November by one of the project's developers. I had the fixed version of the code shortly after that without any effort on my part because I do automatic updates with yum.

Talk about sweet, if I had sent in a bug report like this to a commercial software company I certainly wouldn't have seen such a quick response, a little nuisance like this with a fairly easy work-around wouldn't rate very high on anyone's priority list (but mine), and they probably would have made me pay for a new version to get the fix when it finally did happen! There's a lot of value in such responsive support that makes up for a lack of some of the fancier (but usually unnecessary) features available in some of the commercial computer algebra packages.

Implementing Numerical Methods: an IDE (sort of)

What would an integrated development environment for numerical algorithms look like? To me it looks a lot like Fedora. That’s right, Fedora Linux is your integrated development environment. Oh, separate programs in an operating system isn't integrated enough for you? They ought to be, Python or Bash are right there waiting to glue it all together.

An implementer or developer of numerical methods ought to have a good computer algebra system(CAS) available. This is where the high-level algorithm design needs to take place. All the rest of the low level coding needs to be automated as much as possible. You as the human in the loop need to spend time thinking about the bigger picture and get Maxima to code Fortran for you.

Numerical software needs testing. Lots of rigorous testing. You can use your (CAS) to generate unit tests by evaluating the expressions you converted to Fortran for specific cases, and then converting these answers to Fortran too. Then you can easily wrap those routines in a unit testing framework using F2Py.

This approach lets you automate the generation of the low-level functions that will be in your inner loops (which need to be in Fortran for performance sake). Then use Python's powerful standard library and additional packages for things like parsing input decks, file reading and creation, setting up parallel jobs and generating graphics. All things which can be a real pain in Fortran. The real benefit is that the human effort is kept focused where it is most profitably employed: at the higher levels of abstraction of the mathematical concepts rather than the low level coding.

There it is, a complete "environment" in three building blocks: Maxima, Fortran and Python. Almost completely automated from governing equations in the CAS to low-level number crunching in Fortran. Some human intervention required to bring it all together into a working program, but that’ll be in Python, which is easy.

This is the basic method used in the second half of the magnetron problem. I'll post some more simple examples of the whole work-flow in use after the holidays.

Stupid Human Tricks in Peer Review

I felt like peer review is under attack after reading the second Slashdot article in as many days (1 and 2) about embarrassing failures in peer review of scientific journals/conference articles. The Sokal affair is a pretty well publicized hoax along these lines. The perpetrator wanted to prove a point that articles on post-modern cultural studies were indistinguishable from gobbledygook, surprising no-one outside the field, he was right!

It seems like the above two recent occurrences demonstrate that peer review is in need of an overhaul (or at least a minor upgrade). The second story is about a paper generated by a context free grammar being accepted to a conference. It seems like therein lies a clue to a possible solution.

We need some way to score the "goodness" of a reviewer's work. It's intractable to focus on creating an algorithm for finding "good" original research papers, that basically amounts to implementing some sort of beyond the state-of-the-art artificial intelligence.

What about focusing on "badness"? What if a certain percentage of the articles sent to a reviewer are generated by a context free grammar trained on the archives of relevant journals. These are now known "bad" articles. If the reviewer passes these papers on to publication or presentation then his reputation/score as a reviewer drops. It would need to be a double-blind process. Neither the reviewer nor the institution sending articles for review should know which are true papers and which are generated.

This would be a simple way to check and see if reviewers were paying attention, though it would increase the work-load on a group of folks who are not reimbursed for their time reviewing articles. It would probably improve the results of peer review though, especially if the fact that someone passed along a bogus paper were publicized in the journal itself, right after that page in the front that lists all of the editors and whatnot.

More on Speeding Up Octave

In a previous post we found that speeding up Octave amounted mostly to avoiding for loops. The simplest way to do that is to operate directly on vectors using the built-in operators and functions (which are fast because they are compiled) or cast your problem as a sparse matrix solve. This second option is especially helpful when subsequent calculations depend on previous iterations (the code can't really be vectorized). This option is a very general way of avoiding loops in those cases.

The simple example given previously was a numerical integration of x-squared:

p1(1) = 0;
for( i=2:N )
t = t + dt;
p1(i) = p1( i-1 ) + dt*2*t;
endfor

The way to recast the problem as a sparse matrix solve is to think of p1 as the vector of unknowns, and each iteration of the loop as an equation in the system we want to solve. Writing down the system gives us:


The important detail to remember is to use the functions in Octave to allocate the sparse matrix, or you could easily find yourself writing more really slow for-loops just to create the sparse matrix which you hoped would save lots of time by avoiding for-loops. Talk about the long, slow way around!

Two very useful functions are speye() and spdiag(). The first returns a sparse identity matrix, which is often a good initial building block for many useful operators. The second allows you to place vectors (allocated quickly with the usual vector suspects such as ones() and zeros() ) along the diagonals of the sparse matrix.

# create the main diagonal
A = speye( N );
# alternatively could use spdiag:
# A = spdiag( ones(N,1), 0 );
A = A + spdiag( -ones(N-1,1), -1 ); # add the first sub-diagonal

If your operator isn't banded then you'll need to use spconvert(), which takes as its argument a three (or four if you need a complex result) column matrix. Each row of the argument defines a non-zero entry in the sparse matrix. The first column is the row index, the second column is the column index and the third column is the entry value (fourth column being the imaginary part of the value, if necessary).

Using those three functions should allow you to allocate a sparse matrix in Octave without resorting to for loops (which was why we embarked on this journey to begin with).

This method is counter-intuitive to folks who come from a Fortran (or other compiled language) background, because writing down the loop is the simple, efficient way to solve the problem. It also seems like 'wasting' memory to store all of those redundant coefficients. The timing results speak for themselves though, if you want to stay completely in Octave (or Matlab or Python) sometimes you have to do weird things to get reasonable performance. Of course, if speed really becomes a problem then the inner loops of your calculations need to move to a compiled language that can then be called from Octave, this is a bit more complicated than our little sparse matrix method.

More Edge Detection

I can't really decide on the best way to treat the different channels (red, green, blue) in a color image when doing edge detection. Is it better to just average the magnitude of the gradient in each channel? Treat the channels separately and find red edges, green edges and blue edges? My pragmatic (if ad hoc) choice is to just add them all up, and use a cludge to keep from getting negative gray-scale values.

Here's the Python for gradient-based edges. The magnitude of each channel's gradient is subtracted from 255. Since gray-scale values range from 0 to 255 we use a max() function to set any resulting negative values to 0. The edges detected using this scheme are shown below, on the right.

inpix = img.load()
s = 1.0;
# calculate the gradient in all three channels, sum of squares for mag
for y in xrange(2,h-1):
for x in xrange(2,w-1):
rdx = ( inpix[x+1,y][0] - inpix[x-1,y][0] )/2
gdx = ( inpix[x+1,y][1] - inpix[x-1,y][1] )/2
bdx = ( inpix[x+1,y][2] - inpix[x-1,y][2] )/2
rdy = ( inpix[x,y+1][0] - inpix[x,y-1][0] )/2
gdy = ( inpix[x,y+1][1] - inpix[x,y-1][1] )/2
bdy = ( inpix[x,y+1][2] - inpix[x,y-1][2] )/2
outpix[x,y] = max( 0, 255 - s*( math.sqrt( rdx**2 + rdy**2 ) + math.sqrt( gdx**2 + gdy**2 ) + math.sqrt( bdx**2 + bdy**2 ) ) )

outimg.save(sys.argv[2],"JPEG")

Taking a careful look at the code, you may notice the parameter s floating around in there. This lets you "darken" the edges by choosing something larger than 1. Here's the same image with s=3.0 (on the left):

Like in the previous image processing posts, these examples were made using the Python Imaging Library for image input/output and easy access to the pixels.

My Own Little Pareto Distribution

I signed up for Google Analytics, which collects bunches of neat data. One of the interesting reports is on the number of views each page on your website gets. I plotted them (in Octave of course) with pages across the x-axis, number of views on the y-axis, it looks something like a power law distribution.

x = [11,6,4,2,1,1,1,1,1,1];
bar(x);
print("-dpng","pageviews.png");

Judging by the numbers of pageviews I fear my website is in the trivial many, but that's ok a few people found the octave posts useful.

Asymmetric Complex Step

To solve Laplace's equation with a complex step finite difference we needed to develop asymmetric difference relations to solve on the +/- imaginary planes.

On the plane in the negative imaginary direction we difference centrally in the real direction and forward two steps in the imaginary direction:

And on the plane in the positive imaginary direction we difference centrally in the real direction and backward two steps in the imaginary direction:

We still want the real part of the answer as we did before, but now we have imaginary coefficients for our function values in the real direction. While we have a compact stencil on the real plane (only nearest neighbors are used), we lose that property on either imaginary plane of the solution. This means our system matrix bandwidth is larger than it would be if we had a purely compact stencil for all parts of the solution.

It's fairly easy to calculate arbitrary derivative approximation formulas using Maxima.

/* calculate the coefficients for a finite difference approximation of
a derivative, can include complex steps */

steps : matrix([1,2,%i,2*%i]); /* multiple of the step size h */

/* sum df d2f d3f d4f */
derivs : matrix([0], [1], [0], [0], [0]); /* the rhs for our system */

n : matrix_size( steps );

A : zeromatrix(n[2]+1,n[2]+1);

for j : 1 thru n[2]+1 do
( A[1,j] : 1,
for i : 2 thru n[2]+1 do
(
if j = 1 then A[i,j] : 0 else A[i,j] : steps[1,j-1]^(i-1)/(i-1)!
)
);

invA : invert(A);

coeffs : expand( invA.derivs );
expand( 20*coeffs );

Where the vector steps tells which points will be included in the stencil, and the vector derivs tells which derivative we want to approximate. This example is calculating a real and complex forward difference approximation for the first derivative.

You can download this Maxima batch file here. This example can be run from the command line:

$ maxima -b fd.mac

or using the batch command from an interactive Maxima session:

(%i1) batch("fd.mac")

Latex for Blogging

I've been using htlatex command that comes with the tex4ht package to generate images of nicely typeset equations for use in my blog posts. There are several alternatives for turning latex into html. This article has a decent overview of a few of the methods you might use if you want to have a single tex source file for publishing on the web and on paper. I'm not that serious about my content management. I don't mind a little manual cutting and pasting.

I tried using latex2html, but that is really more suited for processing a large structured document and turning it into a large, structured set of web-pages. All I need is equations, so htlatex is sufficient. If I have a list of equations in 'example.tex', then the command:

$ htlatex example.tex

Produces png image files of all the equations right there in that directory, it even includes the equation labels and alternative text in the generated html, which latex2html does not do. I've noticed that the images generated for a 12pt document look a little better (because they are bigger) when you insert them into a post.

If you're a Fedora user, getting this useful little tool is as easy as

$ yum -y install tetex-tex4ht

Complex Step: Subtractive Cancellation

We showed in an earlier post that approximating first derivatives with complex steps leads to a second order accurate formula that avoids the subtractive cancellation associated with a normal finite difference.

Following the simple convergence study for second derivative approximations we did for cos(). We'll look at the convergence of some first derivative approximation formulas.

The simple complex step approximation is given by

The standard second order finite difference is given by

The 4th order combined complex and real step approximation is

Notice that this formula is not able to avoid subtractive cancellation the way the second order approximation does, but we get a fourth order accurate approximation on a compact stencil.

The convergence of these three formulas for approximating the derivative of cosine is shown in the figure below.

The 4th order scheme runs into subtractive cancellation earlier than the standard 2nd order scheme, but it remains more accurate over the examined range of resolution. The complex step approximation continues to converge as the step size decreases even after the other two formulas diverge.

So for doing sensitivity analysis the second order complex step formula should be used, because only one step needs to be taken, and arbitrarily high precision can be achieved. If you need to approximate a derivative over a region, then the higher order method will pay-off because you can get better accuracy with fewer points.

Is it really O(h**4)?

Over the course of a couple posts (1 and 2) we've shown that you can extend the idea of finite difference approximations to include differences in the imaginary direction. That is you can take complex steps. I presented a formula for the second derivative on a compact stencil (using only nearest neighbours) which I claimed was fourth order accurate. But is it really?

Here's a simple convergence study using cos(), whose second derivative is -cos(). We'll use python to loop over an array with the number of points per wavelength we want to use in our approximation and then calculate a residual, or error, between the analytical solution and our approximation.

for ni in n:
x = 2*pi*arange(0,ni)/(ni-1)
h = x[1]-x[0]
f = cos(x)
analytical_d2f = -cos(x)
# take a positive imaginary step
x_step = x + complex(0,h)
f_pc = cos(x_step)
# take a negative imaginary step
x_step = x - complex(0,h)
f_mc = cos(x_step)
# take a positive real step
x_step = x + h
f_ph = cos(x_step)
# take a negative real step
x_step = x - h
f_mh = cos(x_step)

approx_d2f_c = ( f_ph + f_mh - f_pc.real - f_mc.real)/(2*h*h)
approx_d2f_h = ( f_ph + f_mh - 2*f )/(h*h)

resid_c[i] = sqrt( sum( (analytical_d2f - approx_d2f_c)**2 ) )
resid_h[i] = sqrt( sum( (analytical_d2f - approx_d2f_h)**2 ) )
i += 1

The approximated and analytical second derivatives are shown below for 10 points per wavelength using both a standard central difference with only a real step as well as the complex step formula.

The convergence behaviour for the two approximations is shown below.

Obviously we're getting much better convergence with our complex step formula.

More fun with the PIL

That's the Python Imaging Library. I demonstrated a couple of edge detection techniques (gradient and laplacian) using the PIL to simply read in the image files and make the pixel values conveniently available for twiddling. There's lots of neat stuff in the library other than just image reading/writing utilities. The blend method for instance.
I created a gray-scale image of the magnitude of the gradient (the edges in the image), and then blended it with the original color image. The python to do that takes just two lines:

cblended = Image.blend(outimg.convert("RGB"), img, 0.4)
cblended.save("kuai_laying_color_blend.jpg")

Image.blend() returns an image that is a linear interpolation of the first two arguments (images). The third argument controls if the emphasis is placed on the first image (number closer to zero) or the second image (number closer to one).

Makes it look kind of like a water color, no?

Complex Step Laplace

We can use the results from the previous post about complex step finite differences to solve the 2D Laplace's equation. Instead of solving the equation on a single rectangular grid as we would with normal finite differences, we now solve on three parallel grids (shown below).

One of the grids lies on the real x-y plane, one of the grids is offset slightly in the positive imaginary direction (blue arrow in the figure above), and one of the grids is offset slightly in the negative imaginary direction. We care about the real part of those two imaginary solutions for our second derivative approximation:


The central difference takes care of our solution on the real grid, but what about the two imaginary grids? For those we need asymmetric differences, and I'll put those up in another post.

You might recognize the look of the example mesh if you've ever played around with the 3D modeling/animation program Blender.

Laplacian Edge Detection

In Poor Man's ADC Revisit, I demonstrated gradient based edge detection using Python's Imaging Library to read in a jpg. You can also use the second derivative (a 2D Laplacian operator) to detect edges. Very similar to the gradient based scheme, just change the finite differences to give an approximation to the second derivative rather than the first.

# calculate second derivative for all three channels, sum of squares for mag
for y in xrange(2,h-1):
for x in xrange(2,w-1):
rdx = inpix[x+1,y][0] + inpix[x-1,y][0] - 2*inpix[x,y][0]
gdx = inpix[x+1,y][1] + inpix[x-1,y][1] - 2*inpix[x,y][1]
bdx = inpix[x+1,y][2] + inpix[x-1,y][2] - 2*inpix[x,y][2]
rdy = inpix[x,y+1][0] + inpix[x,y-1][0] - 2*inpix[x,y][0]
gdy = inpix[x,y+1][1] + inpix[x,y-1][1] - 2*inpix[x,y][1]
bdy = inpix[x,y+1][2] + inpix[x,y-1][2] - 2*inpix[x,y][2]
outpix2[x,y] = math.sqrt( rdx*rdx + gdx*gdx + bdx*bdx + rdy*rdy + gdy*gdy + bdy*bdy )

To perform image segmentation it would probably be smart to use the pixel value, the gradient (mag and direction) and the second derivative, no sense in throwing away useful information. Gray-scale image of the magnitude of the second derivative (edges are really where the second derivative changes sign, but an edge tends to have extrema in the second derivative on either side of it) shown below.


Using Psyco or F2Py has been shown on similar problems to give several orders of magnitude speed up over a straight Python implementation as shown above.

Poor Man's ADC Revisit

I wrote a bit ago about using a webcam as an analog-to-digital converter. The really quick hack I put together used Octave's built-in edge() function, which outputs a black and white image of the edges.

A little bit better result can be had with Python's Imaging Library. Here's the basic script to read in the image, calculate the x and y derivatives for the red, blue and green channels, and then set the gray level in the output image to the magnitude of the derivative.

# takes two arguments, input image file, output image file
import sys
import math
import Image

img = Image.open( sys.argv[1] )

w, h = img.size

outimg = Image.new("L",img.size)
outpix = outimg.load()

inpix = img.load()
x = 2;
y = 2;
for y in xrange(2,h-1):
for x in xrange(2,w-1):
rdx = ( inpix[x+1,y][0] - inpix[x-1,y][0] )/2
gdx = ( inpix[x+1,y][1] - inpix[x-1,y][1] )/2
bdx = ( inpix[x+1,y][2] - inpix[x-1,y][2] )/2
rdy = ( inpix[x,y+1][0] - inpix[x,y-1][0] )/2
gdy = ( inpix[x,y+1][1] - inpix[x,y-1][1] )/2
bdy = ( inpix[x,y+1][2] - inpix[x,y-1][2] )/2
outpix[x,y] = math.sqrt( rdx*rdx + gdx*gdx + bdx*bdx + rdy*rdy + gdy*gdy + bdy*bdy );

outimg.save(sys.argv[2],"JPEG")

The resulting gray image looks a lot better than the black and white version generated with Octave (because we aren't throwing away so much information from the original image).

Complex Step**2

I wrote a while back about using a complex step to approximate the first derivative of a function. The neat thing being that there was no subtractive cancellation in the approximation formula as there would be in a normal finite difference. This meant that we could choose very small step sizes without suffering the effects of magnified round-off error.

What about higher order derivatives? The simple result for the first derivative was a second order approximation that only required one function evaluation. Can we achieve the same benefits for a second derivative? The answer is not quite, but it's still pretty good.

The usual way to approximate a second derivative with finite differences is to take a central difference. This uses Taylor series expansions about the location of interest in two directions:


Adding the idea of using complex steps gives two additional points to include in the approximation formula:


Now we just have to solve a linear system to figure out what the coefficients are in our approximation formula:

Based on the Taylor series expansions above, we want the real part of the answer (rather than the imaginary part as was the case with the first derivative). The coefficients are 1/2 for the functions with the real step and -1/2 for the functions with the imaginary step (and zero for the function at x). So we weren't able to avoid subtractive cancellation, but we got an explicit 4th order accurate approximation for the second derivative on a compact stencil!

Sparkle Plenty

I just had a pretty neat problem on my Electrodynamics (course text) mid-term. The problem is to solve for the electric field for two charged conducting spheres of different radii connected by a conducting filament so they reach the same potential.

The result (pdf of full solution) is that the electric field is greater near the surface of the smaller sphere even though it carries less of the total charge. The physical implications of this is that the electric field will be high near the parts of a charged conductor that have a small radius of curvature (ie corners). That's why you get arcing and sparking on forks and crumpled aluminum foil that you put in the microwave.

New Maxima Wiki

My favorite computer algebra system has a new wiki, from the Maxima mailing list (with slight edits to make the links work):

I've set up a new Maxima wiki at http://apps.sourceforge.net/mediawiki/maxima/

You should have a SF account to edit the wiki, see

There are some pages recovered from the old wiki. Please, check the old wiki dump before recreating pages (do not write them from scratch). Eventually I'll copy it to the apps.sourceforge.net/mediawiki/maxima.

Note that the MediaWiki markup differs from the PHPWiki markup. Consult the MediaWiki manual

--
Setting Orange, Aftermath 28 YOLD 3174
Alexey Beshenov http://beshenov.ru/

If you haven't used Maxima before, give it a try. It can do much of what the commercial packages (Mathematica, Maple, MathCad) can do, and it's free software.

As I wrote a while back, it can be really handy for developing numerical software in Fortran or Python (with F2Py).

LED Light Board

The first part of my aeroponics project (overview) is turning those blue and red LED Christmas lights into a grow lamp.

The basic design is a 2 dimensional array of alternating red and blue lights mounted to a piece of white foam board.

Here's a plot of the layout (generated in Octave of course):

And here is the light board as built:

You'll notice two empty holes on the right hand side of the board, the wire between the lights was a really tight fit to meet the spacing I chose (should have checked that a little more closely before drilling all those holes).

Those mini-LEDs look pretty bright, but I'm not sure if it is producing enough light to actually grow a plant, might need to add a string or two. The packaging claims that you can safely plug 43 (!!) of the 60 light strings into a single outlet.

Aeroponics

I've always wanted to build a little aeroponics setup ever since I read some articles about NASA developing aeroponic grow chambers to use on really long space missions. Since we've moved from the gulf coast up to the mid-west, it would be especially nice to have some healthy growing things to brighten up the house during the winter.

There are little kitchen appliances you can buy that grow tomatoes and herbs using an aeroponic method, but where's the fun in just buying one? Much better to build it.

First we need a utility tub as the root chamber where the nutrient ladden fog will be applied.

Now that blue or red LED Christmas lights are common and inexpensive, they make a good light source. They have really low power consumption compared to other types of lights. Why not a white light source? Plants don't use the green part of the spectrum (that's why they look green), so it's a waste of energy to generate white light when we could just generate the red and blue that they do use. To turn a string of ordinary Christmas lights into a plant light we can mount the lights on a sheet of white foam board.

Next we need an ultrasonic humidifier to generate the fog to apply to the roots. Rather than just water in our humidifier though, we need to add some water soluble fertilizer.

We also need to modify some plastic pots so that they become "net pots", basically just slice lots of holes in the sides so the roots can grow out into the fog chamber.

That's it. All told it looks like a home-made aeroponics setup would run about $100, the largest chunk of that being the ultrasonic humidifier ($30).

Poor Man's ADC

Can you use a commodity webcam as an el-cheapo analog to digital converter (ADC)? The folks at slashdot want to know so they can reduce their energy consumption.
Here's the example image:
Octave has plenty of image processing functions in the image package from Octave Forge. Here's the edges detected with the built-in edge() function:

Now we need to perform a smart correlation with the gauge needles so we can map the angle of the needle to a decimal value in [0,10). One way to do it would be to zoom in on the center of the gauge:

Then we can perform a simple least squares regression on the non-zero pixel locations to get a rough estimate of the "slope" of the needle.

needleI = pngread( "needle.png" );
[i,j] = find(needleI(1:35,1:35));
y = 40-j;
x = i;
X = [ ones(length(x),1), x ];
A = X'*X;
b = (X')*y;
beta = A\b;

For the first needle pictured above we get a slope of -0.19643. This seems a tad low, so we probably need to correct for the slant in the original image.

Octave script with all the calculations demonstrated above.

Also check out this book or this page for lots of image processing examples in MATLAB/Octave.

Stupid Google Calculator Tricks

How many fortnights would it take light to travel the circumference of the earth?

What about the speed of light in furlongs per fortnight?

They've got the mass of the proton and the mass of the electron so you can easily calculate their ratio.

I guess we've no need for that gigantic CRC Handbook any more...but what if you need to look up a constant and you're on a desert island with no internet connection, better still pack that CRC just to be safe.

SCons for Latex

Latex is really great for publishing papers with nicely typeset equations and graphics. It automates all of the little formatting stuff and lets you spend time developing the content of your paper rather than wasting effort fiddling with format. I've been using GNU Make for years to process my Latex sources into dvi's and pdf's, but it's always been pretty painful and clumsy (mostly because I'm not a Make guru).

The makefiles for a Latex document can get pretty ugly and complicated especially if your document depends on various data or graphics files. SCons is a new and improved build-tool that implements its configuration files as Python scripts, the file is called SConstruct now instead of Makefile. The great thing from my point of view is that it has built-in support for Latex. Making a pdf from my Latex source file is simple:

env = Environment()
env.PDF('main.tex')

The PDF builder is smart enough to know it needs to run pdflatex and then based on the output possibly run bibtex and then pdflatex again to track down undefined references (or not). All in two lines of Python.

The really neat thing is how easy it is to extend the built-in build environments.

env = Environment()
plot_bld = Builder(action = 'gnuplot < $SOURCE > $TARGET,
suffix = '.png'
src_suffix = '.gp')
env.Append(BUILDERS = {'Plot' : plot_bld})
env.PDF('main.tex')

Now my SCons can automatically update my png graphics files based on gnuplot commands in any files ending with .gp.

Practical Development Environments has a nice little write-up in Chapter 5 about SCons.

EM Flash Cards

I just discovered a great new plug-in (in time for mid-terms) for OpenOffice.org Impress called Open Cards. It is uses the titles of the slides as the question and the body of the slide as the answer to the flashcards. It keeps track of your learning state, has a couple of different learning modes, and seems to use some pretty sophisticated training algorithms.

I put together a set of flashcards for electrodynamics if you're interested in trying it out (of course you need Open Office installed to use the file).

Complex Step

Finite differences are cool, but you are limited by subtractive cancellation (section 3.4: subtractive cancellation exercises). What if you want to make a numerical estimate of the derivative of a function, like a 2D Gaussian:


A finite difference approximation would be (in Octave):

dfdx = ( f(x+h) - f(x) )/ h;

Complex step is even cooler, because you don't have any subtraction (there's no difference), so you can choose a very small step size without loosing accuracy due to subtractive cancelation:

complex_step = complex( 0, 1e-320 );

The derivative is approximated by just the imaginary part:

x = x + complex_step;
dfdx = imag( f(x) )/imag( complex_step );

So the derivative with respect to x looks like this:

And the estimated derivative with respect to y:


This approach is really useful for design sensitivity analysis, and since modern Fortran supports complex types we can even use this method for serious number crunching!

2008 Election Outcome

This is not a political blog, but the Economist has a pretty good article out on John McCain that I felt like commenting on. The last line sums it up: "...pity, there are few better men in American politics".

While he is a very different man than his fellow Naval Academy grad Jimmy Carter, both are men of high integrity, who took that academy training in "duty, honor, country" seriously, and lived it in their public lives after their military service. Though I wasn't alive for the Carter presidency, so I only know it was ineffective from reading about it, I have been alive for President Carter's active work with Habitat for Humanity and his attempts at peace brokering around the world. I think it's safe to say that he embodies Christian ideals of service and peace-seeking. While John McCain is not a paragon of Christian values, he is an exemplar of honesty and sacrifice in public service.

It's too bad that such good men are such unsuccessful politicians in our country. Hopefully Senator McCain's public service after his unsuccessful presidential bid will be as good for the world as President Carter's continues to be following his unsuccessful presidency. Either way, they are a couple of Academy grads I'm proud of (even if they did go to the wrong academy).

Go Air Force, Sink Navy, Beat Army!

A winning combination: Intel and Heineken

I just got a little Atom-based Intel board to play around with and it currently resides in a rubermaid container as its case. I've also been enjoying the new Heineken draught kegs, so I have a few empties sitting in my kitchen floor. This led to the obvious question:

Can a little Atom motherboard

fit inside a Heineken Draught keg?

These new Atom based boards are little mini-itx form factor, that's ~6.93x6.93". The little micro ATX power supplies are ~5x4x3" and a hardrive is ~3.5x5x1". So it might be just a tad to close on the diameter to be able to slide the motherboard right in.

That would be a pretty sweet case though...

The Shuffle

The shuffle, also known as the Fisher's Exact Test, is a permutation test that can be used to estimate the sampling distribution of a statistic without relying on parametric assumptions. This is especially important when sample sizes are small. The other neat thing about permutation tests is that you don't have to know what the distribution of your statistic is. So if you have a really odd function of your data that you want to use rather than one of the classical statistics you can.

Octave has a great built-in function called nchoosek which makes shuffling a breeze. Called with scalar arguments it returns the value of the binomial coefficient, which is the number of ways you can choose k things from n things (k<=n). For fixed n, nchoosek is maximum when k=n/2. That is plotted below for n=2:24.

Notice that's a log-log scale, as n increases it quickly becomes intractable to perform a complete permutation test.

Suppose we have two data vectors, and we want to know if they are from populations with different means. We can use the normrnd() function to draw 8 samples from a normal distribution with 0 mean and 8 samples from a normal distribution with a mean of 1.

n=8;
x1 = normrnd(0,1,n,1);
x2 = normrnd(1,1,n,1);
perms = nchoosek( [x1;x2], n );

We stored all 12870 permutations of the vectors (16 choose 8) in the matrix perms. Now we use the built-in function complement to find the difference of the means under each of those labellings.

for(i=1:length(m1) )
comps(i,:) = complement( perms(i,:), [x1;x2] );
endfor
m1 = mean( perms, 2 ); % take row-wise averages, DIM=2
m2 = mean( comps, 2 ); % take row-wise averages, DIM=2
m_shuff = m1 - m2;

Now we can use the distribution of m_shuff to decide if the difference in the means of our two data vectors is significant.


Octave script with all of these calculations: shuffle.m.

Simple Bayes

I like Bayes theorem, it's really useful. The most intuitive and accessible explanation I've found of using Bayes theorem to solve a problem is in Russell and Norvig's classic, Chapter 20 (pdf) (I just own the first edition, the second edition looks even better).

The initial example they give is about pulling different flavoured candy out of a sack (remember the balls and urn from your basic stats?). They also provide a really good discussion showing how standard least-squares regression is a special case of maximum-likelihood for when the data are generated by a process with Gaussian noise of fixed variance.

Their first example is for estimating parameters in a discrete distribution of candy, but we can apply the same math to estimating the variance of a continuous distribution. Estimating variance is important, lots of times in industrial or business settings the variance of a thing matters as much or more than the average, just check-out all of the press those Six Sigma guys get. That's because it gives us insight into our risk. It helps us answer questions like, "What's our probability of success?" And maybe, if we're lucky, "What things is that probability sensitive to?"

Bayes theorem is a very simple equation:

Where P(h) is the prior probability of the hypothesis, P(d|h) is the likelihood of the data given the hypothesis, and P(h|d) is the posterior probability of the hypothesis given the data.

Octave has plenty of useful built-in functions that make it easy to play around with some Bayesian estimation. We'll set up a prior distribution for what we believe our variance to be with chi2pdf(x,4), which gives us a Chi-squared distribution with 4 degrees of freedom. We can draw a random sample from a normal distribution with the normrnd() function, and we'll use 5 as our "true" variance. That way we can see how our Bayesian and our standard frequentist estimates of the variance converge on the right answer. The standard estimate of variance is just var(d), where d is the data vector.

The likelihood part of Bayes theorem is:

% likelihood( d | M ) = PI_i likelihood(d_i, M_j)
for j=1:length(x)
lklhd(j) = prod( normpdf( d(1:i), 0, sqrt( x(j) ) ) );
endfor
lklhd = lklhd/trapz(x,lklhd); % normalize it

Then the posterior distribution is:

% posterior( M | d ) = prior( M ) * likelihood( d | M )
post_p = prior_var .* lklhd;
post_p = post_p/trapz(x,post_p); % normalize it

Both of the estimates of the variance converge on the true answer as n approaches infinity. If you have a good prior, the Bayesian estimate is especially useful when n is small.

It's interesting to watch how the posterior distribution changes as we add more samples from the true distribution.


The great thing about Bayes theorem is that it provides a continuous bridge from what we think we know to reality. It allows us to build up evidence and describe our knowledge in a consistent way. It's based on the fundamentals of basic probability and was all set down in a few pages by a nonconformist Presbyterian minister and published after his death in 1763.

Octave file for the above calculations: simple_bayes.m

Is Octave Slow?

The answer, like most things worth asking the question about, is "Well, it depends..."

I'm not going to talk about "computer time" vs. "programmer time"; though that's probably one of the most important considerations most of the time (check out Paul Graham's essays if you need convincing). I'll just talk about what takes a long time to compute in Octave, and what trade-offs can be made to improve the situation. We'll dwell mostly on the first tip from the Octave Manual (you'll see it's first for good reason). The other important thing to do is always allocate memory before looping over a vector (eg. x=zeros(n,1)).

Suppose we have a simple re-sampling problem. We would like to estimate the sampling distribution of a statistic of our data. The data could be a simple vector of 1 or 0 representing success or failure of a trial, and we want to estimate the probability of success.

x = [1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0];

One method to solve the problem would be to use a for loop:

X = empirical_rnd(N,x); % get a bootstrap sample from x
for(j=1:10) % timing loop, measure a couple times to get an idea of the
% variation
tic();
for( i=1:N-n ) % loop over the bootstrap samples
p(i) = sum( X(i:i+n-1) )/n;
endfor
fortime(j)=toc();
endfor

With N=20000, this takes 1.09 seconds on my old laptop, that seems kind of slow. The sampling distribution for the probability of success is shown in the figure below.

It is always a good idea to vectorize what you can when in Octave, so the method below does just that.

X = empirical_rnd(x,N,n);
for(j=1:10)
tic();
P = sum(X,2)/n;
vecttime(j) = toc();
endfor

With n=20000, this takes 0.009 seconds on the same old laptop, that's a speed-up of 2 orders of magnitude!

Well, those are trivial examples of vectorizing a calculation to avoid the dreaded for-loop. What happens when subsequent calculations depend on the results of previous iterations?

tic();
p1(1) = 0;
for(i=2:N)
t = t + dt;
p1(i) = p1(i-1)+dt*2*t;
endfor
toc()

This loop integrates x*x numerically, with N=20000 it takes ~0.75 seconds. We can't vectorize, so how do we speed it up? Octave has some good sparse matrix capabilities, maybe we could recast the problem as a sparse matrix solve.

Now we are trading memory for speed. In the for-loop implementation we just have to store the vector p. If we want to use Octave's sparse matrix facilities we need to store the two diagonals of our operator, so that roughly triples the memory requirements. Given the enormous size of modern computer memory, most toy problems should fit (if your problem doesn't fit, why are you still using Octave?).

tic();
A = spdiag( ones(N,1), 0 );
A = A + spdiag( -ones(N-1,1), -1 );
p2 = A\(dt*2*t);
toc()

The direct solution of the simple bi-diagonal system, with N=20000 takes ~0.019 seconds, better than 2 orders of magnitude speed-up over the for-loop implementation. For more complex sparse operators one of the iterative schemes might be appropriate.


The moral: if your problem is small enough to fit into memory, cram it all in and don't use for-loops!

Is Octave slow? Well, it depends, if you use for-loops it is.

Further Reading

A couple more posts on optimizing your Octave code.

• More on Speeding Up Octave (24 Dec 2008)
  
• How to Speed Up Octave (5 Jan 2009)