Here's the paper describing the method.
I think the section on probabilistic carving is most interesting:
One fast and efficient method of removing tetrahedra is by looking at visibility of landmarks. Each triangular face of a tetrahedron is tested in turn against all rays from landmarks to cameras in which they were visible as shown in Figure 3(a). Tetrahedra with one or more faces which intersect with rays are removed. Let Ti represent a triangle in the model, j the keyframe number, k the landmark number and Rj,k the ray from the camera centre at keyframe j to landmark k. Let ν represent the set of all rays with indice pairs (j,k) for which landmark k is visible in keyframe j. For each triangle in the model, the probability that it exists given the set of visible rays can be expressed as:
(1)
(2) In this formulation, Pexist(Ti|ν) takes the value of 0 if any rays intersect the triangle and 1 if no rays intersect the triangle. This yields a very noisy model surface as points slightly below a true surface due to noise cause the true surface to be carved away (Figure 3(c)). Therefore, we design a probabilistic carving algorithm which takes surface noise into account, yielding a far smoother model surface (Figure 3(b) and (d)). Landmarks are taken as observations of a surface triangle corrupted by Gaussian noise along the ray Rj,k , centered at the surface of triangle Ti with variance σ2 . Let x = 0 be defined at the intersection of R
j,k and Ti , and let x be the signed distance along Rj,k , positive towards the camera. Let lk be the signed distance from
x = 0 to landmark Lk . The null hypothesis is that Ti is a real surface in the model and thus observations exhibit Gaussian noise around this surface. The hypothesis is tested by considering the probability of generating an observation at least as extreme as lk :
(3) This leads to a probabilistic reformulation of simple carving:
(4)
(5) If Pexist(Ti|ν) > 0.1, the null hypothesis that Ti exists is accepted, otherwise it is rejected and the tetrahedron containing Ti is marked for removal.
In their recommendations for future work they mention guiding the user to present novel views or revist views that could be erroneous, this seems like a place where the ideas discussed in the Duelling Bayesians post about maximum entropy sampling could be applied.




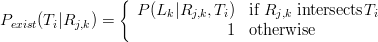
Performance and Use of 3D Imaging Systems
ReplyDeleteSummary:
The use of 3D imaging systems[1] in numerous industry sectors continues to grow. These sectors include widely varying fields such as construction, manufacturing, forensics, and archeology. Of all these sectors, 3D imaging systems have been used primarily in the construction sector; they have used to improve construction productivity by enabling reduced errors and rework, schedule reduction, improved responsiveness to project changes, increased worker safety, and better quality control. Greater use of 3D imaging systems in construction processes is limited by a lack of standards for understanding system performance and delivered information quality. Standards can only be developed when the underlying measurement science is provided which will allow comparable and repeatable evaluation of 3D imaging system performance. Such measurement science would allow for wider acceptance of and increased confidence in the use of 3D imaging systems, and would advance the delivery, whether new or repair, of the nation's physical infrastructure.
[1] a non-contact measurement instrument used to produce a 3D representation (for example, a point cloud) of an object or a site.