FFT-based Convolutions for Oil Extraction Model

The Mobjectivist blog has developed a simple oil production model based on a series of convolutions. Each phase of oil exploitation after discovery, fallow, construction, maturation, and extraction is modeled by first order rate that depends on the amount of stuff at each proceeding stage.

(1)

the solution to which is just

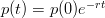(2)

So, for example, the rate of construction depends on the amount of discovered oil that’s been through the fallow stage, the amount of final extraction depends on how much has gotten through each of the proceeding stages. A really convenient way to calculate convolutions is with the FFT, because convolutions are just multiplications in the transformed space. The advantage of an FFT-based approach is the (n log n) scaling of the computational cost (rather than the (n²) scaling of a loop-and-multiply implementation). The draw-back of using an FFT-based convolution is that the FFT assumes the data is periodic, so you need plenty of zero-padding to prevent weird wrap-around effects. The Python to do the required convolution and calculate the simple model is shown below.

 
import scipy as sp 
import scipy.fftpack 
fft = scipy.fftpack.fft 
ifft = scipy.fftpack.ifft 
from scipy.stats.distributions import norm 
from matplotlib import rc 
rc(’text’, usetex=True) 
from matplotlib import pylab as p 
 
 
def exponential_convolution(x, y, r): 
    """Convolve␣an␣exponential␣function␣e^(-r*x)␣with␣y,␣uses␣FFT.""" 
    expo = sp.exp(-r*x) 
    expo = expo / sp.sum(expo) # normalize 
    return(ifft(fft(expo) * fft(y)).real) 
 
nx = 1024 # number of points on the curve 
 
# go out far enough so there’s plenty of entries that are roughly zero 
# at the end, since the FFT assumes periodic data 
 
# years in the model: 
x = sp.linspace(0.0, 400.0, nx) 
 
# a simple oil extraction model where everything is a first order rate 
# the ’discovery’ distribution: 
y = norm.pdf(x, loc=50, scale=10) 
# ’fallow’: 
y_conv_1 = exponential_convolution(x, y, 0.04) 
# ’construction’: 
y_conv_2 = exponential_convolution(x, y_conv_1, 0.04) 
# ’maturation’: 
y_conv_3 = exponential_convolution(x, y_conv_2, 0.04) 
# ’extraction’: 
y_conv_4 = exponential_convolution(x, y_conv_3, 0.04) 
 
 
p.plot(x, y, label="discovery") 
p.plot(x, y_conv_1, label="fallow") 
p.plot(x, y_conv_2, label="construction") 
p.plot(x, y_conv_3, label="maturation") 
p.plot(x, y_conv_4, label="extraction") 
p.legend(loc=0) 
p.xlabel("time") 
p.ylabel("rate") 
p.savefig("model.png") 
p.show()

Figure 1 shows the results.

---

Figure 1: Simple Convolution-based Oil Extraction Model

---